GCSE Physics - Motor Effect #79
Summary
TLDRIn this video, we explore the motor effect, which describes how a current-carrying wire experiences a force when placed in a magnetic field. The direction of this force can be determined using Fleming's Left-Hand Rule, which involves positioning the left hand to represent the magnetic field, current, and force. The strength of the force is calculated using the equation F = BIL, where B is magnetic flux density, I is current, and L is the length of the wire. The video illustrates these concepts through examples and practical calculations, helping viewers understand how current and magnetic fields interact.
Takeaways
- 😀 A current-carrying wire in a magnetic field experiences a force due to the interaction between the wire's magnetic field and the external magnetic field.
- 😀 The wire needs to be at a 90-degree angle to the magnetic field to experience the maximum force. If it is at a slight angle, the force will be reduced, and if aligned with the field, no force will be experienced.
- 😀 Fleming's Left-Hand Rule is used to determine the direction of the force on the wire by aligning the thumb (force), first finger (magnetic field), and second finger (current).
- 😀 In Fleming's Left-Hand Rule, the first finger represents the direction of the magnetic field, the second finger represents the direction of current, and the thumb shows the direction of the force.
- 😀 To use Fleming's Left-Hand Rule, practice moving your hand or body to find the correct orientation for determining the force direction.
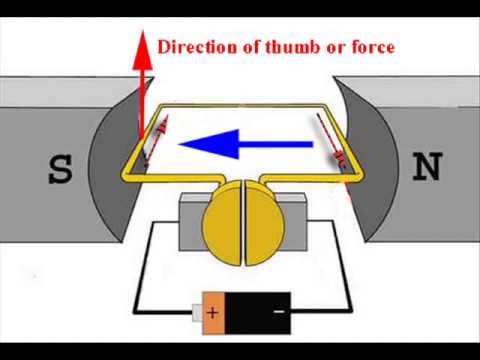
- 😀 A common demonstration of the motor effect involves a rolling metal rail between the poles of a horseshoe magnet, where the current in the rail interacts with the magnetic field to produce a force.
- 😀 The direction of the force in the horseshoe magnet scenario can be determined using Fleming's Left-Hand Rule by pointing the first finger downward (magnetic field) and the second finger towards the observer (current), resulting in the force direction indicated by the thumb.
- 😀 The strength of the force on the wire can be calculated using the formula F = BIL, where F is the force, B is the magnetic flux density (in teslas), I is the current (in amperes), and L is the length of the wire (in meters).
- 😀 The formula F = BIL is given in exams, so you don't need to memorize it. The key is to use the correct units for each variable.
- 😀 Example calculation: A 10 cm wire with a 5 A current in a 0.4 T magnetic field at a 90-degree angle experiences a force of 0.2 N after converting the length into meters and applying the formula.
Q & A
What is the motor effect?
-The motor effect refers to the phenomenon where a current-carrying wire in the presence of a magnetic field experiences a force. This force is a result of the interaction between the magnetic field created by the wire and the external magnetic field.
How does the angle of the wire affect the force it experiences in a magnetic field?
-The force is maximized when the wire is at a right angle (90 degrees) to the magnetic field. If the wire is at a slight angle, the force will be reduced. If the wire is aligned in the same direction as the magnetic field, no force will be felt.
What is Fleming's left-hand rule and how is it used?
-Fleming's left-hand rule helps determine the direction of the force on a current-carrying wire in a magnetic field. To use the rule, extend your left hand with the thumb, first finger, and second finger at right angles. The first finger points in the direction of the magnetic field, the second finger in the direction of the current, and the thumb points in the direction of the force on the wire.
What happens when the current flows through metal rails in a magnetic field?
-When current flows through metal rails placed between the poles of a magnet, the magnetic field generated by the current interacts with the external magnetic field, resulting in a force on the rails. The force causes motion, as seen in the example where one of the rails can move.
How do you calculate the force on a wire in a magnetic field?
-The force can be calculated using the equation F = BIL, where F is the force in newtons, B is the magnetic flux density in teslas, I is the current in amperes, and L is the length of the wire in meters.
What units are used in the equation F = BIL?
-In the equation F = BIL, the units are: F (force) in newtons, B (magnetic flux density) in teslas, I (current) in amperes, and L (length of the wire) in meters.
Why is it important for the wire to be at 90 degrees to the magnetic field when calculating the force?
-When the wire is at 90 degrees to the magnetic field, the force is maximized. If the wire is at any other angle, the force will be less than the maximum possible value.
How do you convert centimeters to meters in the context of the equation F = BIL?
-To convert centimeters to meters, divide the length in centimeters by 100. For example, 10 centimeters becomes 0.1 meters.
What is the significance of the magnetic flux density (B) in determining the force on a wire?
-The magnetic flux density (B) represents the strength of the magnetic field. A higher magnetic flux density results in a greater force on the wire, assuming the current and the length of the wire are constant.
Can the motor effect be observed without using Fleming's left-hand rule?
-While it is possible to observe the motor effect visually, Fleming's left-hand rule provides a reliable method to accurately determine the direction of the force, making it an essential tool for understanding and predicting the behavior of current-carrying wires in magnetic fields.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)