Materi Lengkap Translasi (Pergeseran) || TRANSFORMASI GEOMETRI

Summary

This video tutorial focuses on the concept of geometric transformations, specifically translation (or shifting). The instructor explains the basic principles of translation, covering how points, curves, and shapes are moved with a fixed distance and direction without altering their form. It includes practical examples such as translating triangles, points, and curves, along with the use of translation matrices. The video also demonstrates how to perform translation through formulas and provides creative methods for translating equations. Additionally, the concept of composition of translations is explored, providing a deeper understanding of how multiple transformations can be combined.

Takeaways

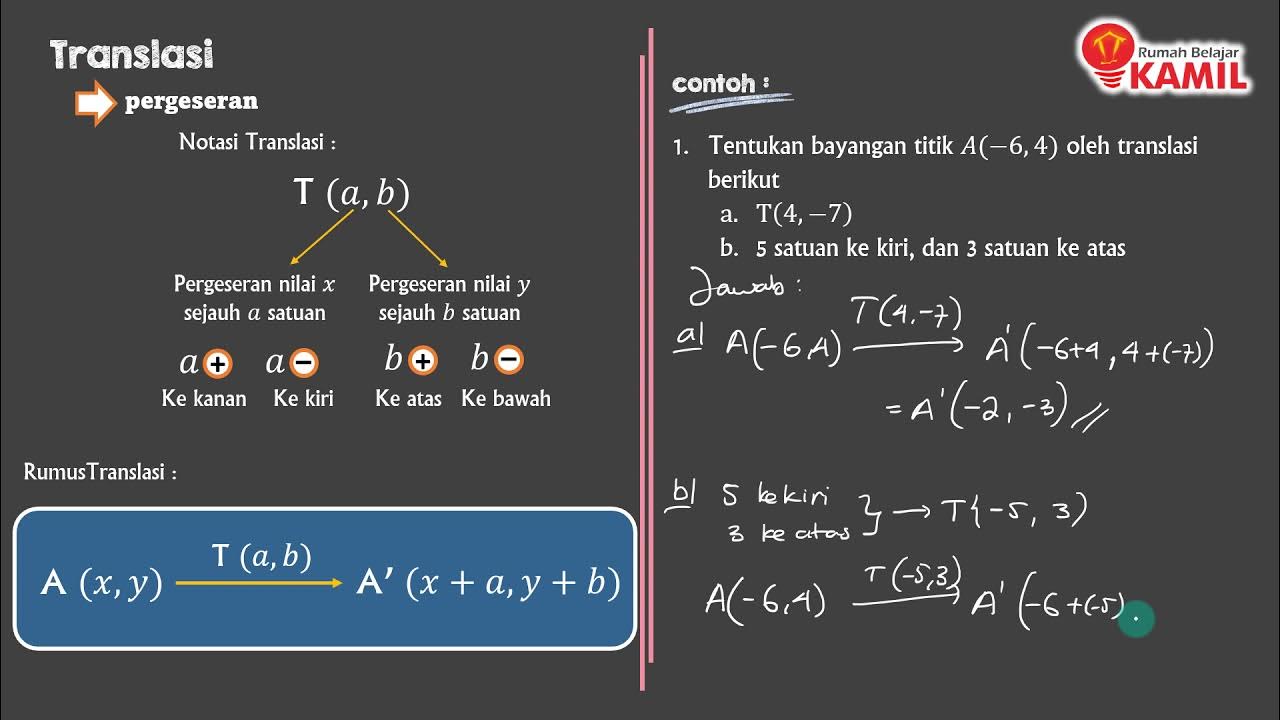
• 😀 Translation is a geometric transformation where an object moves a fixed distance in a specified direction without changing its shape.
• 😀 The formula for translation involves adding a translation vector (k, b) to each point of an object, represented as (x + k, y + b).
• 😀 Translation works for points, curves, and other geometric objects, and it preserves their shape and orientation.
• 😀 Translating a point involves adding the translation vector to the coordinates of the original point.
• 😀 The translation matrix is a method to compute translations, and it is often represented as a vector added to the original coordinates.
• 😀 To find the translated image of a point, we add the vector values to the coordinates of the original point.
• 😀 Example: If a point (x, y) is translated by the vector (k, b), the new point will be (x + k, y + b).
• 😀 In translation of curves, the same principle applies: each point on the curve is shifted by the translation vector.
• 😀 The composition of translations involves applying multiple translation vectors in succession. The result is a single translation represented by the sum of the vectors.
• 😀 When translating equations of lines or curves, the translation vector can be substituted into the equation to find the translated curve or line.
• 😀 The lecturer encourages practicing with various translation problems, including translating points, triangles, and equations of lines or curves.

Q & A

What is geometric transformation, and what are its main types?

Geometric transformation refers to the process of changing the position, shape, or size of a figure. The main types are translation, reflection, rotation, and dilation.

What does translation (or 'pergeseran') mean in geometry?

Translation in geometry refers to shifting a figure from one position to another without changing its shape or size. It involves moving every point of the figure by the same distance and in the same direction.

What is the role of a translation matrix in geometric transformations?

A translation matrix is used to perform the translation by adding a constant to the coordinates of each point in the object being translated, which shifts its position without altering its shape.

How is the translation of a point calculated?

To translate a point, you add the corresponding translation vector's components (usually denoted as (k, l)) to the point's coordinates. The new coordinates are found by summing the original point's coordinates with the translation vector.

What does the notation 'x' with an accent (x') indicate in the context of translations?

The notation 'x' with an accent (x') represents the translated or transformed coordinates of a point. It indicates the new position of the point after applying the translation.

How is the translation of curves or lines different from that of points?

The translation of curves or lines follows the same principle as point translation, where each point of the curve or line is translated. For a line, the equation is adjusted to reflect the translation, but the shape and orientation remain unchanged.

Can you explain the concept of translation composition in geometry?

Translation composition involves applying multiple translations sequentially. The result is a combined translation, where the final transformation is the sum of the individual translation vectors.

What is the process for translating a line, such as the equation 'x + 2y = 4'?

To translate a line, substitute the translated coordinates (x' and y') into the equation, adjusting for the translation vector. The result is a new equation that represents the translated line, but with the same slope as the original.

How do you calculate the translation of a point, for example, from (2,3) to (3,7)?

To calculate the translation, subtract the original point’s coordinates from the translated point’s coordinates to find the translation vector. In this case, subtracting (2, 3) from (3, 7) gives a translation vector of (1, 4).

What happens to the equation of a curve after it undergoes translation?

After translation, the equation of the curve will be adjusted by adding or subtracting values corresponding to the translation vector. The form of the equation will change, but the curve's general shape and orientation remain the same.