04 Diédrico: Angulo Diedro Pirámide cuadrada: resolución
Summary
TLDREste video enseña cómo resolver el ejercicio de una pirámide de base cuadrada con un ángulo diedro de 110 grados. El proceso comienza con el dibujo de la base de la pirámide, seguida de la proyección del ángulo diedro. Se utilizan herramientas como un transportador y compás para calcular los puntos claves y las tangentes necesarias para construir la pirámide. A lo largo de los pasos, se explica cómo llevar la altura y ajustar las dimensiones para lograr una pirámide con las medidas correctas. Es una guía práctica para realizar construcciones geométricas precisas en 3D.
Takeaways
- 😀 Dibuja una pirámide con base cuadrada de 60 mm, asegurándote de que las diagonales formen un ángulo de 45 grados con la línea de tierra.
- 😀 El ángulo diedro entre las caras de la pirámide es de 110 grados. Se debe abatir este ángulo con una bisectriz de 55 grados en cada lado.
- 😀 Utiliza un transportador de ángulos para realizar el abatimiento y no dibujar el arco capaz, ya que solo se necesita la mitad de este arco.
- 😀 El ángulo límite es de 180 grados, lo que afecta la forma de la pirámide, ya que los ángulos más grandes no tienen solución geométrica en este caso.
- 😀 La proyección del vértice sobre la línea de tierra se utiliza para construir la circunferencia con un radio igual a la distancia del vértice a la intersección de las diagonales.
- 😀 Las tangentes a la circunferencia deben ser construidas con precisión, no a ojo, para asegurar que las medidas sean exactas.
- 😀 Evita hacer construcciones geométricas a ojo, ya que las tolerancias pueden verse afectadas, especialmente cuando se trabajan con distancias específicas.
- 😀 Una vez que las tangentes se han trazado, prolonga las líneas hasta encontrar el vértice de la pirámide.
- 😀 La solución final muestra la pirámide con la base cuadrada, el vértice y las líneas tangentes correctamente construidas.
- 😀 La altura de la pirámide debe ser de 120 mm, lo cual se establece después de localizar el vértice y ajustarlo según el enunciado del problema.
Q & A
¿Cuál es el primer paso en el ejercicio para construir la pirámide?
-El primer paso es dibujar un cuadrado con un lado de 60 mm y asegurarse de que las diagonales del cuadrado formen un ángulo de 45 grados con la línea de tierra.
¿Cómo se debe orientar el cuadrado para este ejercicio?
-El cuadrado debe orientarse de manera que sus diagonales formen un ángulo de 45 grados con la línea de tierra, asegurando que las aristas paralelas estén alineadas con el plano vertical.
¿Qué se debe hacer después de dibujar el cuadrado?
-Después de dibujar el cuadrado, el siguiente paso es aplicar el ángulo diedro especificado en el ejercicio. En este caso, el ángulo es de 110 grados, que se debe dividir a la mitad para facilitar el proceso.
¿Cómo se divide el ángulo diedro de 110 grados?
-El ángulo de 110 grados se divide en dos partes iguales de 55 grados cada una, lo que facilita su construcción geométrica sin necesidad de dibujar el arco capaz completo.
¿Qué herramienta es necesaria para medir y aplicar el ángulo en el ejercicio?
-Es necesario un transportador de ángulos para medir y aplicar los 55 grados de la mitad del ángulo diedro, así como un compás para hacer las construcciones geométricas.
¿Qué es el 'arco capaz' mencionado en el ejercicio y cómo se usa?
-El arco capaz es el lugar geométrico de los puntos desde los cuales se ve un segmento bajo un ángulo específico. En este ejercicio, se menciona como una forma de calcular los ángulos, pero se simplifica al dividir el ángulo de 110 grados en dos partes iguales.
¿Cómo se determina la tangencia en este ejercicio?
-Se determina haciendo una circunferencia que tiene como radio la distancia desde el vértice del ángulo diedro hasta el centro de la pirámide. Luego, se dibujan las tangentes de esta circunferencia para localizar el vértice de la pirámide.
¿Qué paso sigue después de determinar las tangencias?
-Después de determinar las tangentes, se une el punto de tangencia con el vértice de la pirámide y se prolongan las líneas para completar la estructura.
¿Cómo se ajusta la altura de la pirámide en este ejercicio?
-La altura de la pirámide, que se especifica como 120 mm, se mide desde el vértice de la pirámide hacia arriba y se traza para ajustar la forma de la pirámide a la altura requerida.
¿Qué ocurre si no se usa una herramienta precisa como el transportador o el compás?
-Si no se utilizan herramientas precisas como el transportador o el compás, la tolerancia de las construcciones geométricas puede verse afectada, lo que puede resultar en una solución incorrecta o imprecisa.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
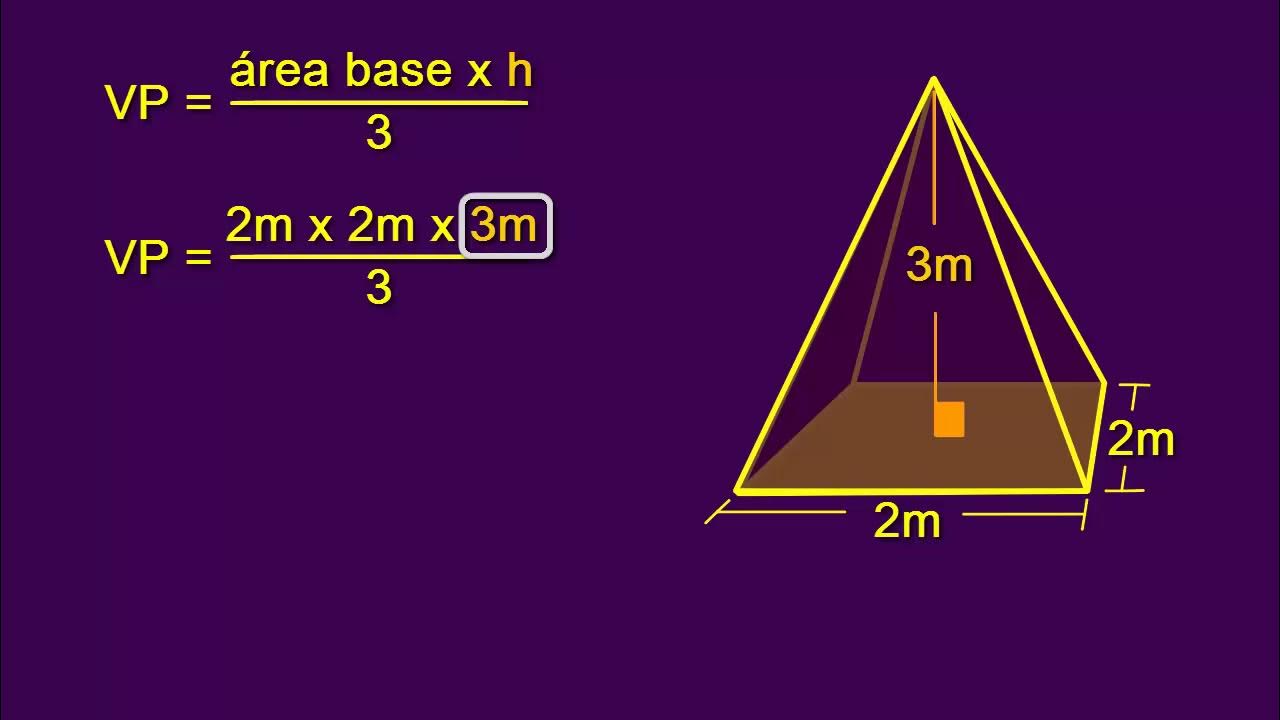
Cálculo del Volumen de una Pirámide de Base Cuadrada

⭐ Determinar el Valor de los Ángulos Complementarios | Video 11

Ángulos en la circunferencia │ ángulo inscrito

1 Ejercicio de longitud de arco

CIRCUNFERENCIA: Teoremas Fundamentales de Los Ángulos

¿Cómo calcular la pendiente y el ángulo de inclinacion?_1
5.0 / 5 (0 votes)
