1.3 How Write and Analyze Algorithm

Summary

This video script explores the essential concepts of algorithm writing and analysis. It emphasizes the importance of focusing on the logical structure of algorithms rather than language-specific details like data types or variable declarations. The script delves into key evaluation criteria such as time complexity (how fast the algorithm runs) and space complexity (how much memory it uses), while also considering other factors like data transfer, power consumption, and CPU usage. The goal is to create efficient algorithms by analyzing their performance in terms of both time and space, based on the needs of the project or system.

Takeaways

• 😀 An algorithm is an abstract procedure for solving problems and doesn't require language-specific details like data types or variable declarations.
• 😀 A program is a specific implementation of an algorithm in a programming language, requiring syntax, data type declarations, and proper variable handling.
• 😀 In an algorithm, you don't have to worry about the minor details such as temporary variables, which are required in a program.
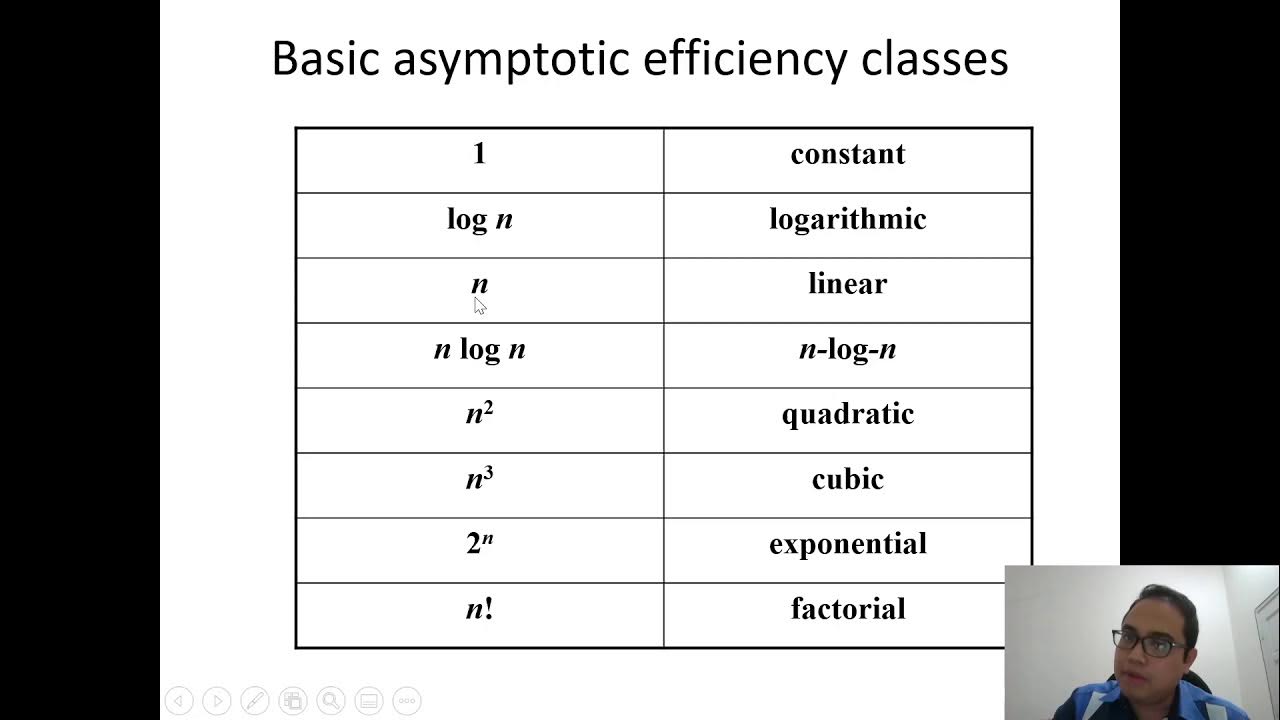
• 😀 Time complexity is a measure of how much time an algorithm takes to execute based on the size of the input, often represented as a function.
• 😀 Each statement in an algorithm is typically assumed to take one unit of time for time complexity analysis, even if in actual programming, statements may require more.
• 😀 The time complexity of an algorithm is often represented in terms of constant values (e.g., O(1)) when the number of operations doesn’t depend on the input size.
• 😀 Space complexity refers to how much memory an algorithm uses, and is influenced by the number of variables and data structures employed.
• 😀 An algorithm’s space complexity can also be constant (O(1)) if it only uses a fixed number of variables regardless of input size.
• 😀 Additional factors such as network consumption, data transfer, power usage, and CPU load may be considered when analyzing an algorithm for specific applications.
• 😀 In performance-sensitive scenarios, deeper analysis may be required to understand how an algorithm affects system resources such as CPU registers and power consumption.

Q & A

What is the main difference between an algorithm and a program?

An algorithm is a high-level, language-agnostic procedure to solve a problem, whereas a program is a specific implementation of that algorithm in a programming language with syntax, data types, and variable declarations.

Why is syntax flexibility important in writing algorithms?

Syntax flexibility allows the writer to focus on the logic and problem-solving aspect of the algorithm rather than being constrained by the specific rules of a programming language. The main goal is for the algorithm to be understandable to others, not necessarily to follow a fixed language syntax.

What are the two primary criteria for analyzing an algorithm?

The two primary criteria for analyzing an algorithm are time efficiency (how fast the algorithm runs) and space efficiency (how much memory the algorithm uses).

How is time efficiency measured in algorithm analysis?

Time efficiency is measured by counting the units of time each operation takes. In simple cases, each statement in the algorithm is assumed to take one unit of time, leading to a time function that describes the algorithm's overall time complexity.

What is the importance of space efficiency in algorithm analysis?

Space efficiency is crucial because it determines how much memory the algorithm will consume during execution. The number of variables used in the algorithm is counted to estimate its space complexity, which should be kept as low as possible to avoid resource strain.

Why might additional factors like data transfer and power consumption be important in algorithm analysis?

These factors are important because modern algorithms often run on networks or devices with limited resources. For example, high data transfer rates can increase costs, and excessive power consumption can reduce the device's battery life. These factors become critical when the algorithm is deployed in real-world systems, such as mobile devices or cloud applications.

How does the level of detail in algorithm analysis affect the results?

The level of detail in algorithm analysis affects the accuracy and applicability of the results. A high-level analysis might provide rough estimates (e.g., assuming constant time for each operation), while a more detailed analysis would account for lower-level factors like machine code instructions or memory management, which can impact performance more precisely.

What does it mean when time complexity is said to be constant (O(1))?

Constant time complexity (O(1)) means that the algorithm's execution time does not depend on the size of the input. Whether the input is small or large, the algorithm will always take the same amount of time to complete.

In the provided example, how is time complexity calculated?

In the example, time complexity is calculated by assuming each statement takes one unit of time. Since there are three statements, the total time complexity is constant, denoted as O(1), which means it takes a fixed amount of time regardless of input size.

How is space complexity evaluated in the given algorithm example?

Space complexity is evaluated by counting the number of variables used in the algorithm. In the provided example, there are three variables (parameters and local variables), so the space complexity is constant, represented as O(1), meaning the space required does not increase with input size.