Equilíbrio de corpo extenso rígido | estática
Summary
TLDRIn this engaging physics lesson, Professor Douglas Gomes explores the principles of equilibrium for rigid bodies, emphasizing both translational and rotational balance. Through practical examples, like the forces acting on a bar supported at two points, he explains the importance of torques and how they contribute to maintaining balance. The video also touches on real-life applications of torque, such as steering a car and pedaling a bicycle. By the end, viewers learn how to calculate forces and torques to achieve equilibrium, offering valuable insights into the mechanics behind balanced systems.
Takeaways
- 😀 Equilibrium in physics involves two main conditions: the net force must be zero, and the net torque must also be zero for rotational equilibrium.
- 😀 When studying rigid bodies, the force resultants need to be balanced for the object to be in translational equilibrium, but this doesn't automatically mean the object is in rotational equilibrium.
- 😀 Torque is the rotational equivalent of force, and it depends on the magnitude of the force and the distance from the pivot point (lever arm).
- 😀 A torque is zero if the force is applied at the point of rotation, and the direction of rotation (clockwise or counterclockwise) matters when balancing torques.
- 😀 In the case of a rigid body, if the forces result in a net torque in one direction (clockwise), the opposing forces must create an equal and opposite torque (counterclockwise) to maintain equilibrium.
- 😀 A simple example of rotational torque is turning a steering wheel, where both hands create opposing torques to rotate the wheel.
- 😀 The center of mass of a uniform object, like a bar, coincides with its center of gravity, and it’s crucial for calculating forces in static equilibrium.
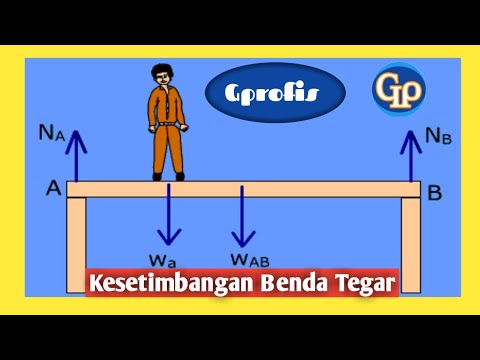
- 😀 In an example of a bar supported at two points, the sum of the vertical forces at the supports must equal the weight of the bar, and the torques must balance around a chosen pivot point.
- 😀 For static equilibrium, when calculating torques, it’s essential to consider the geometry of the object and the distances from the pivot to the force applications.
- 😀 When solving for unknown forces in equilibrium problems, such as finding the forces at the supports of a bar, you can use the conditions of force and torque balance to determine them.
- 😀 The problem of a uniform bar supported at two points illustrates the practical application of torque and force balance, where the force at one support might be greater than the other, depending on the location of the center of mass.
Q & A
What is the first condition for static equilibrium of a rigid body?
-The first condition for static equilibrium is that the resultant force acting on the body must be zero. This means the sum of all the forces acting on the body in different directions must cancel each other out.
Does the first condition of equilibrium apply to extended objects (not just point masses)?
-Yes, the first condition of equilibrium applies to extended objects as well. The resultant force must be zero for the object to be in translational equilibrium, regardless of whether it is a point mass or a rigid body.
What is the second condition for static equilibrium?
-The second condition for static equilibrium is that the sum of all the torques acting on the object must be zero. This ensures that the object does not rotate. The torques in the clockwise direction must balance out the torques in the counterclockwise direction.
What is the difference between force and torque?
-Force is a push or pull that can cause an object to move or change its motion, whereas torque is a rotational force that causes an object to rotate around an axis. Torque depends on both the force applied and the distance from the axis of rotation (lever arm).
What is the significance of the center of mass in the context of static equilibrium?
-The center of mass is the point where the total mass of an object can be considered to be concentrated for the purpose of analyzing its motion or equilibrium. For a homogeneous body, the center of mass is at its geometric center, and it is where the force of gravity acts.
How do you calculate the torque of a force applied to an object?
-The torque (τ) is calculated by multiplying the force (F) by the distance from the axis of rotation (r), also known as the lever arm. The formula is τ = F * r. The direction of the torque is determined by whether the force causes a clockwise or counterclockwise rotation.
In the case of a beam supported at two points, how do you find the forces at the supports?
-To find the forces at the supports, you need to apply both the conditions for static equilibrium: (1) the sum of all vertical forces must equal zero, and (2) the sum of all torques about any point must equal zero. By setting up equations based on these conditions, you can solve for the unknown forces at each support.
In the example of a 10-meter beam with a mass of 12 kg, why do the forces at the supports differ?
-The forces at the supports differ because the beam is not perfectly balanced at the center. The torque created by the weight of the beam is not symmetrical, so the forces at the supports must compensate for the uneven distribution of weight to prevent the beam from rotating.
Why is it important to use both hands to steer a car in terms of torque?
-Using both hands to steer a car ensures that the forces are applied symmetrically, creating an effective torque that makes it easier to rotate the steering wheel. It also provides more control and stability, reducing strain on the steering mechanism and improving safety.
What is the relationship between the force at a point and the torque in the example of the beam supported by two points?
-The force at each support must balance both the weight of the beam and the torques generated by that weight. The torque created by the weight depends on the distance from the axis of rotation. The forces at the supports are determined by balancing these torques to ensure no rotation occurs, with one support exerting a greater force due to its position relative to the center of mass.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Rotational Equilibrium Introduction (and Static Equilibrium too!!)
F23 - Kesetimbangan Benda Tegar ,cara mudah memahami.

Introductory Rotational Equilibrium Problem

FISIKA KELAS XI || Kesetimbangan || DINAMIKA ROTASI & KESETIMBANGAN BENDA TEGAR

Qual a diferença entre potência (cavalos) e torque?

L18 - Dyanamics - Lesson 18 - Rigid Body Kinematics
5.0 / 5 (0 votes)