Capacitors and Kirchhoff: Crash Course Physics #31
Summary
TLDRIn this episode of Crash Course Physics, we explore Kirchhoff’s Laws, which are essential for analyzing complex electrical circuits. The Junction Rule explains how current behaves at circuit junctions, while the Loop Rule helps determine voltage drops across resistors in loops. The episode also delves into capacitors in DC circuits, explaining their behavior when connected in series and parallel. By applying these laws and principles, we can solve for currents and voltages in intricate circuits. The episode concludes with a look at how capacitors store and release charge, a crucial concept for understanding transient conditions in circuits.
Takeaways
- 😀 Kirchhoff’s Junction Rule states that the sum of all currents entering a junction is equal to the sum of all currents leaving the junction.
- 😀 Kirchhoff’s Loop Rule asserts that the sum of all changes in potential around a loop equals zero, ensuring energy conservation in a circuit.
- 😀 Batteries in a circuit increase potential, while resistors cause a drop in potential, similar to a roller coaster's ups and downs.
- 😀 A complex circuit with multiple batteries and resistors requires Kirchhoff's Laws for accurate analysis, beyond simple Ohm's law.
- 😀 To apply Kirchhoff’s Junction Rule, label all junctions and currents in the circuit, then use the rule to relate currents at those junctions.
- 😀 In loop analysis, the direction of current flow should be carefully considered, as it determines how voltage gains and drops are calculated.
- 😀 The equivalent capacitance of capacitors in parallel is the sum of their individual capacitances, unlike resistors in parallel.
- 😀 Capacitors in series reduce the overall capacitance of the circuit, as opposed to resistors in series, which increase the total resistance.
- 😀 Capacitors temporarily store charge in a DC circuit and release it later, which can influence the transient behavior of a circuit.
- 😀 Understanding how capacitors behave in both series and parallel configurations is essential for analyzing more complex DC circuits.
- 😀 Kirchhoff’s Laws, combined with Ohm’s law, allow for a comprehensive approach to solving circuits with multiple components and energy sources.
Q & A
What is the main topic of this episode of Crash Course Physics?
-The main topic of this episode is the analysis of more complex DC circuits using Kirchhoff’s Laws and capacitors, along with how capacitors behave when connected in series and parallel.
How does Kirchhoff’s Junction Rule work?
-Kirchhoff’s Junction Rule states that the sum of all currents entering a junction in a circuit must equal the sum of all currents leaving the junction. This reflects the conservation of charge.
What does Kirchhoff’s Loop Rule state?
-Kirchhoff’s Loop Rule states that the sum of all changes in potential (voltage) around a closed loop in a circuit must equal zero, which reflects the conservation of energy.
How is Kirchhoff’s Loop Rule related to the operation of a battery in a circuit?
-The battery in a circuit provides a voltage gain, and this energy is lost across resistors as voltage drops. Kirchhoff’s Loop Rule ensures that the sum of these voltage gains and drops around a loop equals zero.
Why is it important to label currents and junctions when applying Kirchhoff’s Laws?
-Labeling currents and junctions is crucial because it helps set up the equations for the circuit, allowing you to track how current flows and apply the conservation laws correctly in solving for unknowns.
How do you apply Kirchhoff’s Junction Rule in solving for currents in a circuit?
-You apply the Junction Rule by setting up an equation that equates the sum of currents entering a junction to the sum of currents leaving the junction. This gives you relationships between different current values in the circuit.
What happens to the total capacitance when capacitors are connected in parallel?
-When capacitors are connected in parallel, the total or equivalent capacitance increases. This is because the total charge is the sum of the charges held by each individual capacitor.
What is the effect of connecting capacitors in series on the overall capacitance?
-When capacitors are connected in series, the overall capacitance decreases. The total capacitance is less than that of the smallest individual capacitor in the series.
How do you calculate the equivalent capacitance of capacitors connected in parallel?
-The equivalent capacitance of capacitors in parallel is simply the sum of their individual capacitances, as each capacitor in parallel holds the same voltage and contributes to the total charge.
Why does the charge remain the same for capacitors connected in series?
-In a series connection, the charge remains the same on all capacitors because current can’t flow through the capacitors; instead, charge is redistributed across the plates, ensuring that the charge on each capacitor remains equal.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
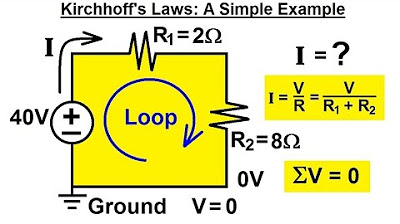
Electrical Engineering: Basic Laws (9 of 31) Kirchhoff's Laws: A Simple Example
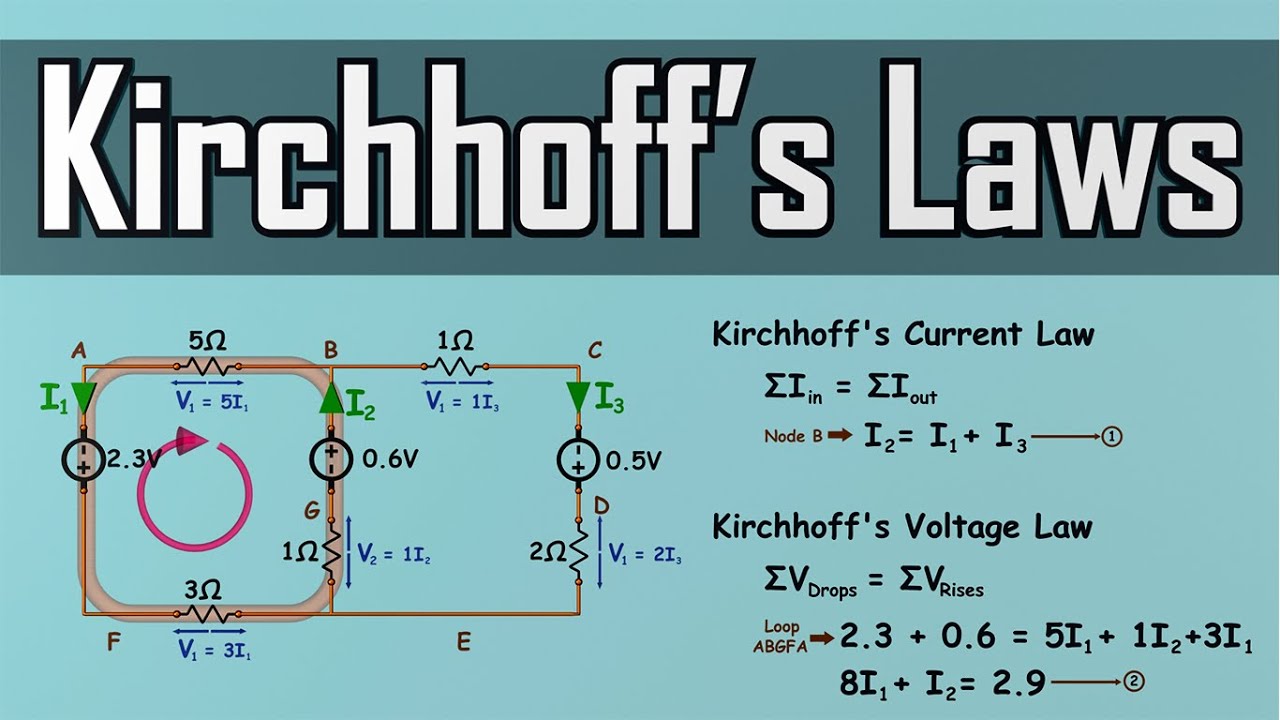
Kirchhoff's Laws - How to Solve a KCL & KVL Problem - Circuit Analysis

KVL and KCL Examples (Circuits for Beginners #12)

SK#2c: Pemodelan Sistem dengan Persamaan Differensial

Kirchhoff's Current Law (KCL) Explained

Circuit Analysis: Crash Course Physics #30
5.0 / 5 (0 votes)