Medidas de dispersión
Summary
TLDREn estadística, las medidas de dispersión son fundamentales para entender cómo se distribuyen los datos. Estas incluyen el rango, que mide la diferencia entre el valor más alto y el más bajo; el rango intercuartílico, que analiza la dispersión en la mitad de los datos; y la varianza, que mide la dispersión total, aunque su resultado está en unidades al cuadrado. La desviación estándar, calculada como la raíz cuadrada de la varianza, es útil al expresarse en las mismas unidades que los datos. Por último, el coeficiente de variación compara la desviación estándar con la media, proporcionando un porcentaje que describe la magnitud de la dispersión en relación con la media.
Takeaways
- 😀 Las medidas de dispersión son esenciales para entender cómo se agrupan y distribuyen los datos.
- 😀 El rango mide la diferencia entre el valor más alto y el más bajo de un conjunto de datos, y es el método más simple de dispersión.
- 😀 El rango intercuartílico se calcula entre los cuartiles primero y tercero, representando la dispersión del 50% central de los datos.
- 😀 La varianza mide el promedio de las distancias cuadradas entre los datos y la media, dándole más peso a las desviaciones más grandes.
- 😀 A diferencia de otras medidas, la varianza se expresa en unidades al cuadrado, lo que puede hacerla difícil de interpretar.
- 😀 La desviación estándar es la raíz cuadrada de la varianza, y permite expresar la dispersión en las mismas unidades que los datos originales.
- 😀 El coeficiente de variación es una medida relativa que expresa la desviación estándar como un porcentaje de la media.
- 😀 Para calcular el coeficiente de variación, se divide la desviación estándar entre la media y el resultado se multiplica por 100.
- 😀 La desviación estándar y el coeficiente de variación son útiles para comparar la dispersión en diferentes conjuntos de datos.
- 😀 Las medidas de dispersión, como el rango y la varianza, son cruciales para analizar la variabilidad y la distribución de los datos en estadísticas.
Q & A
¿Qué son las medidas de dispersión en estadística?
-Las medidas de dispersión indican el grado en que los datos se separan o agrupan en una distribución. Son fundamentales para entender cómo se distribuyen las observaciones en un conjunto de datos.
¿Por qué es importante conocer las medidas de dispersión?
-Es importante conocer las medidas de dispersión porque nos permiten evaluar la variabilidad de los datos y hacer comparaciones entre diferentes conjuntos de datos, lo que ayuda en la interpretación de la información estadística.
¿Qué es el rango en términos de dispersión?
-El rango es una medida de dispersión que se obtiene calculando la diferencia entre el valor más alto y el más bajo de un conjunto de datos. Es una medida sencilla de entender, pero limitada, ya que solo considera dos valores.
¿Cuál es la principal limitación del rango?
-La principal limitación del rango es que solo toma en cuenta los dos valores extremos (el más alto y el más bajo) del conjunto de datos, lo que lo hace sensible a valores atípicos y no refleja toda la distribución de los datos.
¿Qué es el rango intercuartílico?
-El rango intercuartílico mide la dispersión entre el 25% inferior y el 25% superior de los datos, es decir, entre el primer y el tercer cuartil. Se utiliza para entender la dispersión de la mitad central de los datos, excluyendo los valores extremos.
¿Cómo se calcula el rango intercuartílico?
-El rango intercuartílico se calcula como la diferencia entre el valor del tercer cuartil (Q3) y el primer cuartil (Q1), es decir, Rango intercuartílico = Q3 - Q1.
¿Qué es la varianza y cómo se calcula?
-La varianza mide la dispersión de los datos respecto a la media. Se calcula restando cada valor del conjunto de datos a la media, elevando esa diferencia al cuadrado, sumando todos los resultados y luego dividiendo entre el número total de observaciones.
¿Por qué se eleva al cuadrado cada distancia en el cálculo de la varianza?
-Se eleva al cuadrado cada distancia para asegurar que todas las diferencias sean positivas, lo que elimina los posibles efectos de las desviaciones negativas. Además, al elevar al cuadrado, se otorga mayor peso a las desviaciones más grandes.
¿Por qué la varianza se expresa en unidades cuadradas?
-La varianza se expresa en unidades cuadradas porque se calcula elevando al cuadrado las diferencias entre los valores y la media. Esto significa que su unidad de medida es el cuadrado de la unidad de los datos originales, lo que puede ser problemático para la interpretación directa.
¿Qué es la desviación estándar y cómo se relaciona con la varianza?
-La desviación estándar es la raíz cuadrada de la varianza. Esta medida se utiliza para superar el problema de las unidades cuadradas de la varianza, ya que la desviación estándar se expresa en las mismas unidades que los datos originales, facilitando su interpretación.
¿Qué es el coeficiente de variación y cómo se calcula?
-El coeficiente de variación es una medida que expresa la desviación estándar como un porcentaje de la media. Se calcula dividiendo la desviación estándar entre la media y multiplicando el resultado por 100. Se utiliza para comparar la dispersión de diferentes conjuntos de datos con diferentes unidades o magnitudes.
¿Cuál es la principal ventaja de usar el coeficiente de variación?
-La principal ventaja del coeficiente de variación es que permite comparar la variabilidad de diferentes conjuntos de datos, incluso si tienen diferentes unidades de medida o escalas, ya que convierte la dispersión en un porcentaje relativo a la media.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
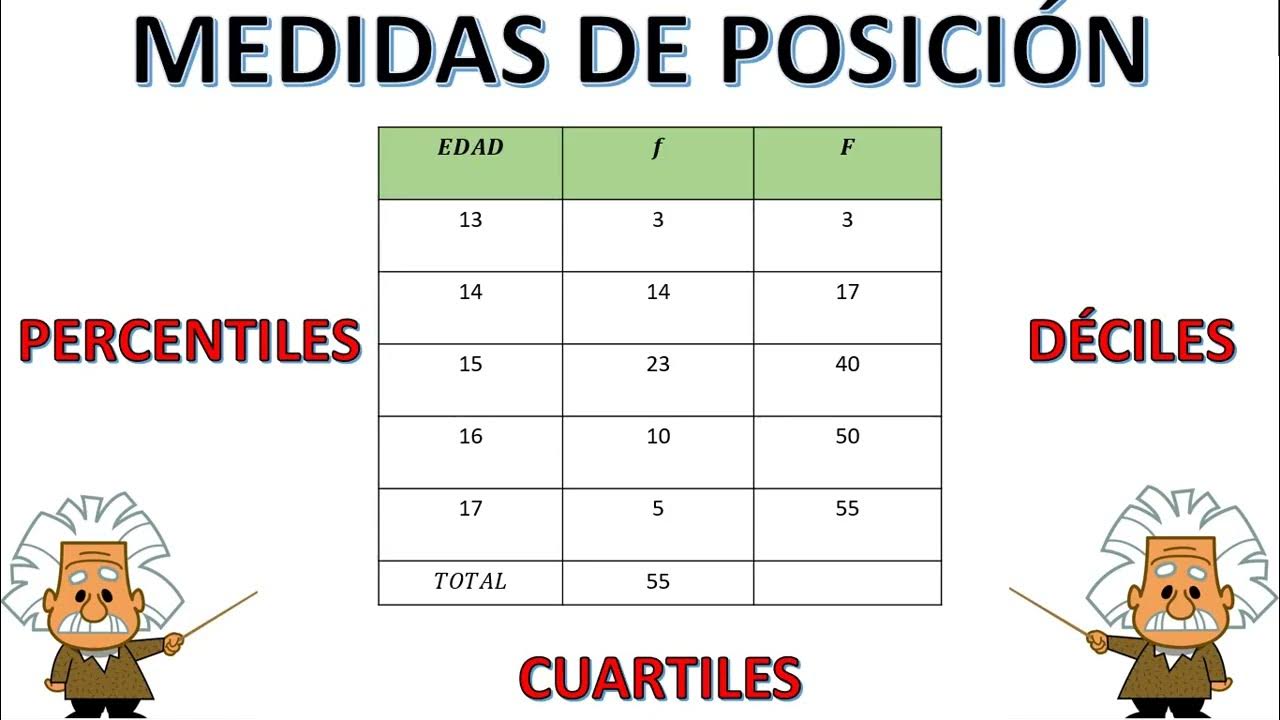
MEDIDAS DE POSICIÓN: PERCENTILES, DECILES Y CUARTILES #estadistica #deciles #percentiles

Qué es la Desviación Estándar - Típica

Conceptos estadísticos básicos

Medidas Descriptivas Ejemplo

Estadística Descriptiva: Medidas de Síntesis (I). Módulo 2

MEDIA, MODA Y MEDIANA Super facil | Medidas de tendencia central
5.0 / 5 (0 votes)
