Differentialquotient berechnen – Limes, Ableitung Beispiel
Summary
TLDRIn diesem Video wird erklärt, wie man mit dem Differenzialquotienten Berechnungen durchführt und die Ableitung einer Funktion an einer beliebigen Stelle \( x_0 \) ermittelt. Schritt für Schritt wird der Prozess anhand eines Schemas veranschaulicht, um die Aufgabe verständlicher zu machen. Der Fokus liegt darauf, wie man den Differenzialquotienten anwendet, um die Ableitung zu finden, und anschließend wird die Steigung an einer bestimmten Stelle berechnet. Der zweite Teil der Aufgabe wird ebenfalls besprochen, um den gesamten Lösungsprozess zu verdeutlichen.
Takeaways
- 🧮 Der Differentialquotient dient zur Berechnung der Ableitung einer Funktion an einer beliebigen Stelle x₀.
- 📐 Die Steigung einer Funktion an einer bestimmten Stelle kann mit Hilfe des Differentialquotienten ermittelt werden.
- 📝 Der Differentialquotient sieht auf den ersten Blick kompliziert aus, kann aber Schritt für Schritt vereinfacht werden.
- 🔢 Die Berechnung der Ableitung erfolgt durch den Grenzwert, wenn x gegen x₀ läuft.
- 📊 Im Differentialquotienten stehen im Zähler und Nenner jeweils Differenzen, die symmetrisch aufgebaut sind.
- ✏️ Im ersten Schritt werden die Funktionswerte f(x) und f(x₀) in die Formel eingesetzt.
- ➗ Danach wird der Bruch vereinfacht, indem man den Zähler und Nenner so weit wie möglich kürzt.
- 🔄 Die dritte binomische Formel kann verwendet werden, um den Zähler zu faktorisieren und den Bruch weiter zu vereinfachen.
- 📉 Nachdem der Bruch vereinfacht wurde, wird der Grenzwert gebildet, um zur endgültigen Ableitung zu gelangen.
- 📈 Die Steigung der Funktion an der Stelle x₀ wird durch Einsetzen des Wertes x₀ in die Ableitungsfunktion bestimmt.
Q & A
Was ist das Hauptthema des Videos?
-Das Hauptthema des Videos ist, wie man Berechnungen mit dem Differenzialquotienten durchführt, um die Ableitung einer Funktion an einer beliebigen Stelle zu bestimmen.
Warum wird der Differenzialquotient oft als abschreckend empfunden?
-Der Differenzialquotient wird oft als abschreckend empfunden, weil er auf den ersten Blick komplex aussieht, besonders für Anfänger in der Mathematik.
Was ist die Hauptaufgabe, die im Video erklärt wird?
-Die Hauptaufgabe besteht darin, mit Hilfe des Differenzialquotienten die Ableitung der Funktion f an einer beliebigen Stelle x0 zu berechnen.
Was bedeutet es, den Grenzwert für den Differenzialquotienten zu bilden?
-Den Grenzwert zu bilden bedeutet, dass man untersucht, was mit dem Quotienten passiert, wenn x immer näher an x0 herankommt, um so die Ableitung zu bestimmen.
Warum werden im Video keine Ableitungsregeln verwendet?
-Im Video werden keine Ableitungsregeln verwendet, weil das Thema Ableitungen gerade erst eingeführt wird, und der Fokus auf der Anwendung des Differenzialquotienten liegt, bevor man die Regeln lernt.
Wie wird der Differenzialquotient im Video definiert?
-Der Differenzialquotient wird als Grenzwert eines Bruchs definiert, bei dem im Nenner (x - x0) steht und im Zähler (f(x) - f(x0)).
Was ist der erste Schritt bei der Berechnung des Differenzialquotienten?
-Der erste Schritt besteht darin, die Werte f(x), f(x0) und x0 in den Differenzialquotienten einzusetzen, ohne dabei f(x) oder x0 zu verändern, es sei denn, x0 ist explizit gegeben.
Wie wird der Bruch im Differenzialquotienten vereinfacht?
-Der Bruch wird vereinfacht, indem zunächst die Klammern im Zähler aufgelöst und dann der Bruch gekürzt wird, falls gemeinsame Faktoren in Zähler und Nenner auftreten.
Welche Rolle spielt die binomische Formel bei der Vereinfachung des Differenzialquotienten?
-Die dritte binomische Formel wird verwendet, um den Zähler in eine faktorisierte Form zu bringen, wodurch es möglich wird, den Nenner zu kürzen.
Wie wird der Grenzwert letztendlich berechnet?
-Der Grenzwert wird berechnet, indem x gegen x0 läuft, was bedeutet, dass man am Ende den Ausdruck für f(x) durch f(x0) ersetzt und die übrigen Terme zusammenfasst.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Bestimmung von Tangenten - Die Tangentengleichung | Differenzialrechnung | Flip the Classroom

Ableitung Grundlagen
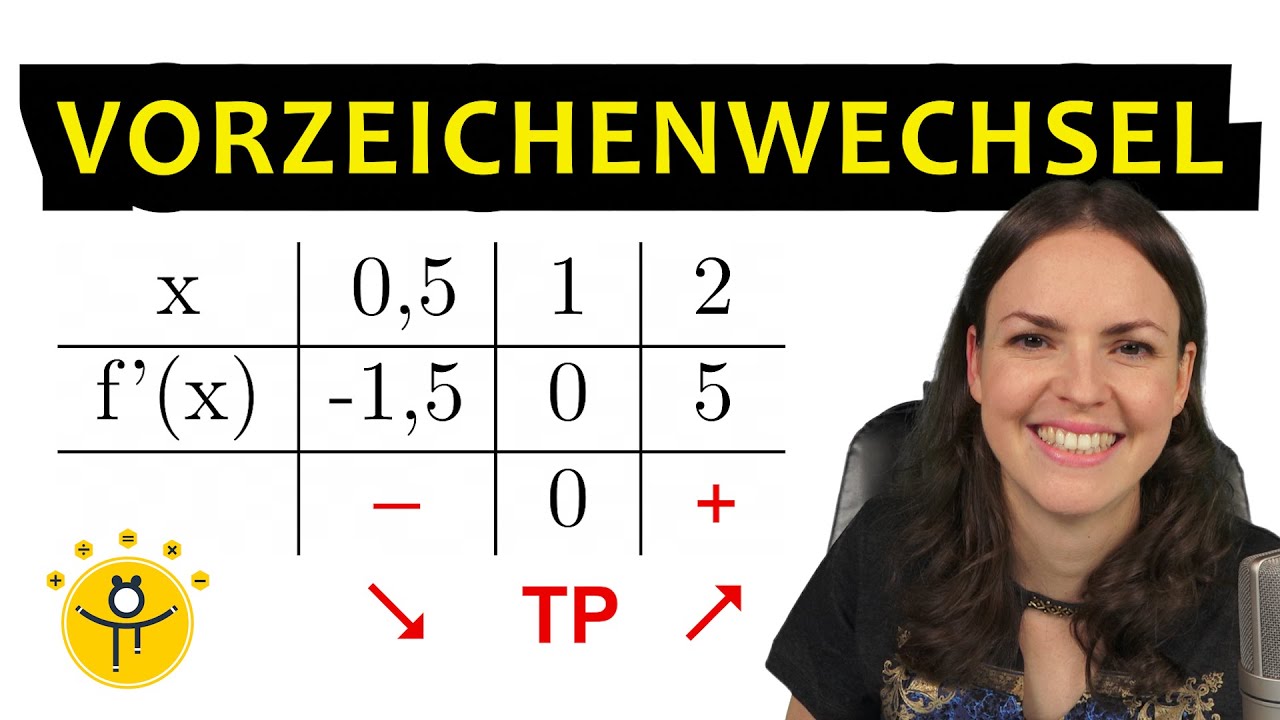
EXTREMA Vorzeichenwechsel Kriterium – Hochpunkt Tiefpunkt berechnen
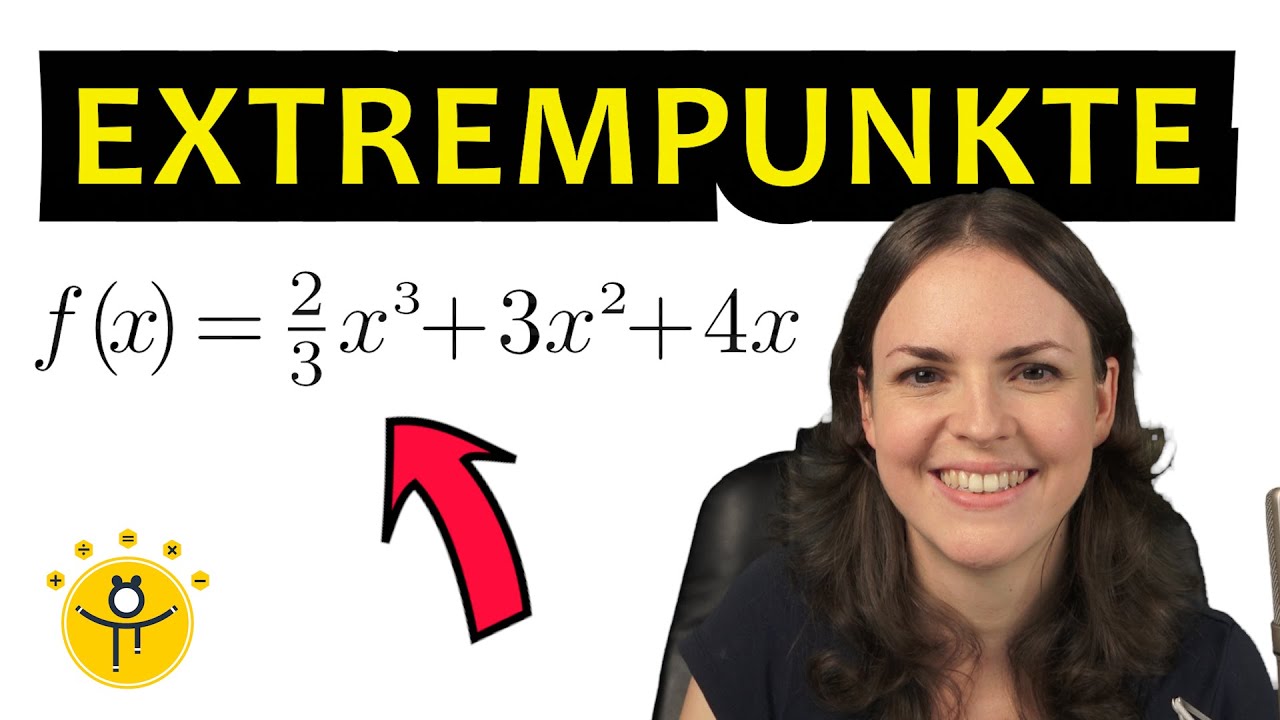
EXTREMPUNKTE berechnen für Anfänger – Ableitung ganzrationaler Funktionen bestimmen

Graphisches Ableiten - Graph der Ableitung skizzieren | Differenzialrechnung | Flip the Classroom

NULLSTELLEN durch Ausklammern und pq Formel bestimmen – Nullstellen berechnen Ausklammern
5.0 / 5 (0 votes)
