Math Antics - Ratios And Rates
Summary
TLDRIn this Math Antics lesson, viewers learn about ratios and their practical applications. The video explains that ratios are essentially fractions but used to compare two different things, such as sandwiches to people at a picnic. The lesson clarifies the concept of ratios through everyday examples like fruit stands, baking recipes, and screen dimensions. It also covers rates, including how to convert them to unit rates for easier comparison. By the end of the lesson, viewers will understand how ratios and rates function in real-world scenarios and how to work with them in math.
Takeaways
- 😀 A ratio is a comparison of two numbers by division, showing how two numbers relate to each other.
- 😀 Ratios are similar to fractions, but ratios describe the relationship between two different things (e.g., sandwiches and people), while fractions represent parts of a whole.
- 😀 When written as '1 to 2', the ratio shows the relationship between two quantities, like '1 sandwich per 2 people'.
- 😀 Ratios can be written in different formats: either as '1:2' or '1/2', representing the same relationship.
- 😀 Ratios are used to describe real-world situations, such as comparing apples to oranges (5:3) or the ingredients in a recipe (2:1).
- 😀 A rate is a type of ratio that involves time, such as 40 miles per hour (40 miles/1 hour).
- 😀 Rates are often converted to unit rates, where the denominator is 1, to make comparisons easier.
- 😀 Unit rates help in comparing speeds, like determining which car is faster when their rates are given in different time intervals.
- 😀 A rate like '40 miles per 3 hours' can be converted into a unit rate by dividing the top number by the bottom number, resulting in '40 miles per hour'.
- 😀 Understanding ratios and rates is useful in everyday life, from planning a picnic (1:2 sandwiches to people) to calculating travel speeds (miles per hour).
- 😀 The bottom number of a rate often represents a unit of time (seconds, hours, days), and it is usually converted to 1 for easier comparison between different rates.
Q & A
What is a ratio?
-A ratio is a comparison of two numbers by division, showing how two numbers relate to each other.
How are ratios and fractions similar?
-Ratios and fractions are mathematically similar because both involve division, but they are used differently. A fraction shows a part of something, while a ratio shows the relationship between two different things.
What’s the difference between a fraction and a ratio?
-In a fraction, both numbers refer to the same thing, such as parts of a whole. In a ratio, the two numbers refer to different things, such as sandwiches and people in a picnic example.
What does a ratio like 1:2 represent?
-A ratio like 1:2 means for every 1 of one thing, there are 2 of another thing. For example, in a picnic, it could mean 1 sandwich for every 2 people.
Why might you use a ratio in real life?
-Ratios are used in many real-world situations to compare quantities. Examples include comparing the number of apples to oranges at a fruit stand or the amount of flour to sugar in a recipe.
What does the ratio 16:9 represent in relation to a TV or computer screen?
-The ratio 16:9 represents the aspect ratio of a screen, showing the width (16 inches) compared to the height (9 inches) of the screen.
What is a rate?
-A rate is a special type of ratio that usually compares one quantity to a unit of time, like miles per hour or dollars per hour.
How is a rate like '40 miles per hour' written as a ratio?
-The rate '40 miles per hour' is a ratio of 40 miles to 1 hour, or 40:1.
What is a unit rate, and why is it useful?
-A unit rate is a rate where the bottom number is 1, making it easier to compare different rates. For example, converting 120 miles per 3 hours to a unit rate gives 40 miles per 1 hour.
How can you convert a rate like '120 miles per 3 hours' into a unit rate?
-To convert a rate to a unit rate, divide the top number by the bottom number. For example, 120 miles ÷ 3 hours = 40 miles per hour.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Matemática Para Concursos - Aula 05 - Razão e Proporção - Parte I

MATH 5 || QUARTER 3 WEEK 1 | PERCENT AND ITS RELATIONSHIP TO FRACTIONS, RATIOS, AND DECIMAL NUMBERS

Konsep Rasio Hal 83-94 Bab 3 RASIO kelas 7 SMP Kurikulum Merdeka
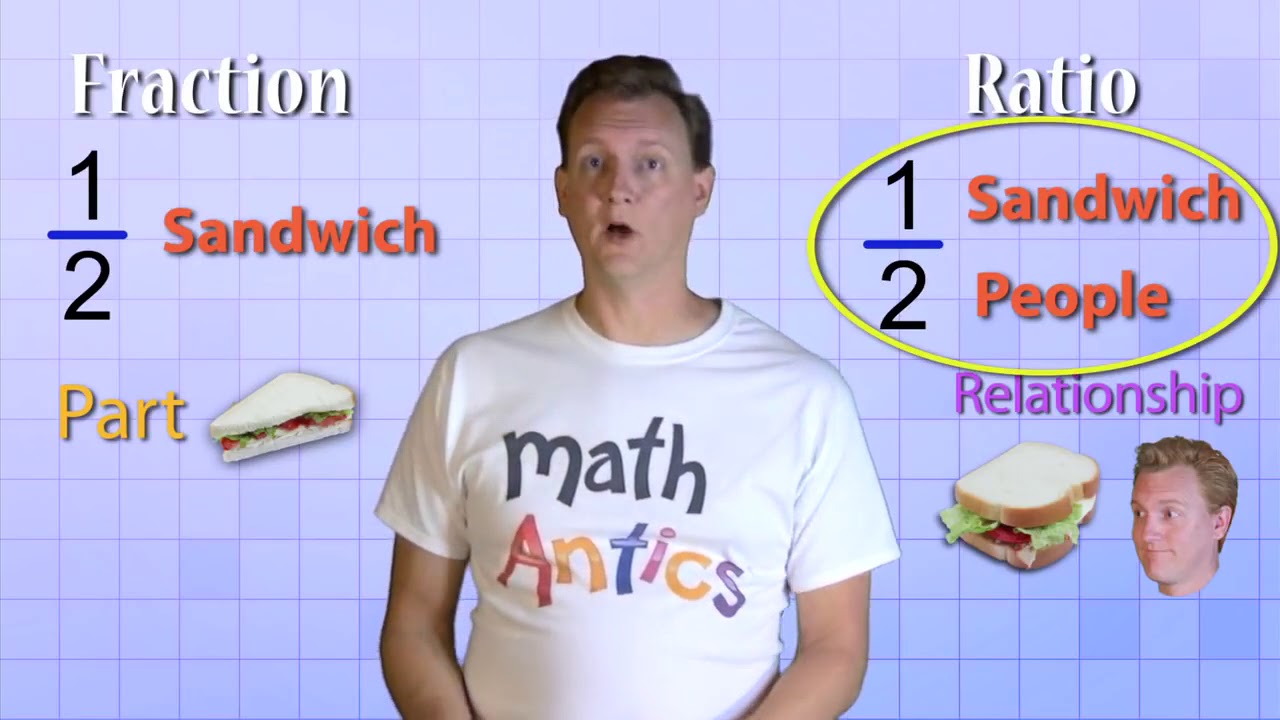
Math Antics Ratios And Rates

BASFIN1 - Debt Management Ratios

Unit 2 - Lesson 2 (Proportion)
5.0 / 5 (0 votes)