AP Physics 1 Circular Motion and Gravitation Review
Summary
TLDRThis video provides a comprehensive review of circular motion and gravitation for AP Physics 1. It explains uniform circular motion, highlighting how velocity changes direction while speed remains constant, leading to centripetal acceleration directed toward the center of the circle. The video further details the forces involved in circular motion, such as tension and normal force, and illustrates these concepts with examples like roller coasters and ferris wheels. It concludes with an exploration of Newton's law of gravitation, emphasizing the relationship between mass, distance, and gravitational force, as well as the dynamics of satellites in orbit.
Takeaways
- 😀 Uniform circular motion occurs when an object travels in a circle at a constant speed and radius.
- 🔄 The time to complete one full circle is calculated using the formula T = 2πR/V.
- ➡️ Velocity in circular motion is always tangent to the circle, while acceleration points towards the center.
- 🏃♂️ Centripetal acceleration is given by a_c = V²/R, directing the acceleration towards the center.
- 🔗 Centripetal force is not a new force; it results from other forces acting on the object, like tension or normal force.
- ❌ If centripetal force is removed, the object will move off in a straight line due to inertia.
- 🌌 Newton's law of gravitation states that the force between two masses is proportional to their masses and inversely proportional to the square of their distance apart.
- ⚖️ The gravitational force is equal and opposite for both masses involved, adhering to Newton's third law.
- 🌍 The acceleration due to gravity (g) at the surface of a planet can be calculated using g = G(M/R²), where G is the universal gravitational constant.
- 🛰 For orbiting objects, gravitational force provides the centripetal force necessary for circular motion, leading to the relation T² ∝ R³ for orbital periods.
Q & A
What defines uniform circular motion?
-Uniform circular motion occurs when an object travels in a circle at a constant speed while maintaining a constant radius.
How is the time taken to complete one circle calculated?
-The time T to complete one circle is calculated using the equation T = 2πR / V, where R is the radius and V is the speed of the object.
Why does an object in circular motion experience acceleration?
-An object in circular motion experiences acceleration because its velocity is changing direction, even if its speed remains constant.
What is centripetal acceleration, and how is it expressed mathematically?
-Centripetal acceleration is the acceleration directed towards the center of the circle, given by the formula a_c = V² / R.
What role do forces play in circular motion?
-Forces are responsible for causing circular motion, and the net force, or centripetal force, must always point toward the center of the circle.
What happens to an object if the centripetal force is removed?
-If the centripetal force is removed, the object will move off in a straight line due to inertia, as it is no longer subject to net force.
How do gravitational forces relate to circular motion?
-Gravitational forces can provide the centripetal force necessary for circular motion, such as in the case of satellites orbiting a planet.
What is Newton's law of gravitation?
-Newton's law of gravitation states that the gravitational force between two masses is proportional to the product of their masses and inversely proportional to the square of the distance between them.
How does the acceleration due to gravity (g) relate to the mass and radius of a planet?
-The acceleration due to gravity on the surface of a planet can be expressed as g = GM/R², where G is the universal gravitational constant, M is the mass of the planet, and R is its radius.
What is the relationship between the period of an orbiting object and the radius of its orbit?
-The period of an orbiting object is proportional to the cube of the radius of its orbit, meaning that as the distance from the planet increases, the orbital period increases.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

(New) AP Physics 1 - Unit 1 Review - Kinematics - Exam Prep
AP Physics C: Kinematics Review (Mechanics)
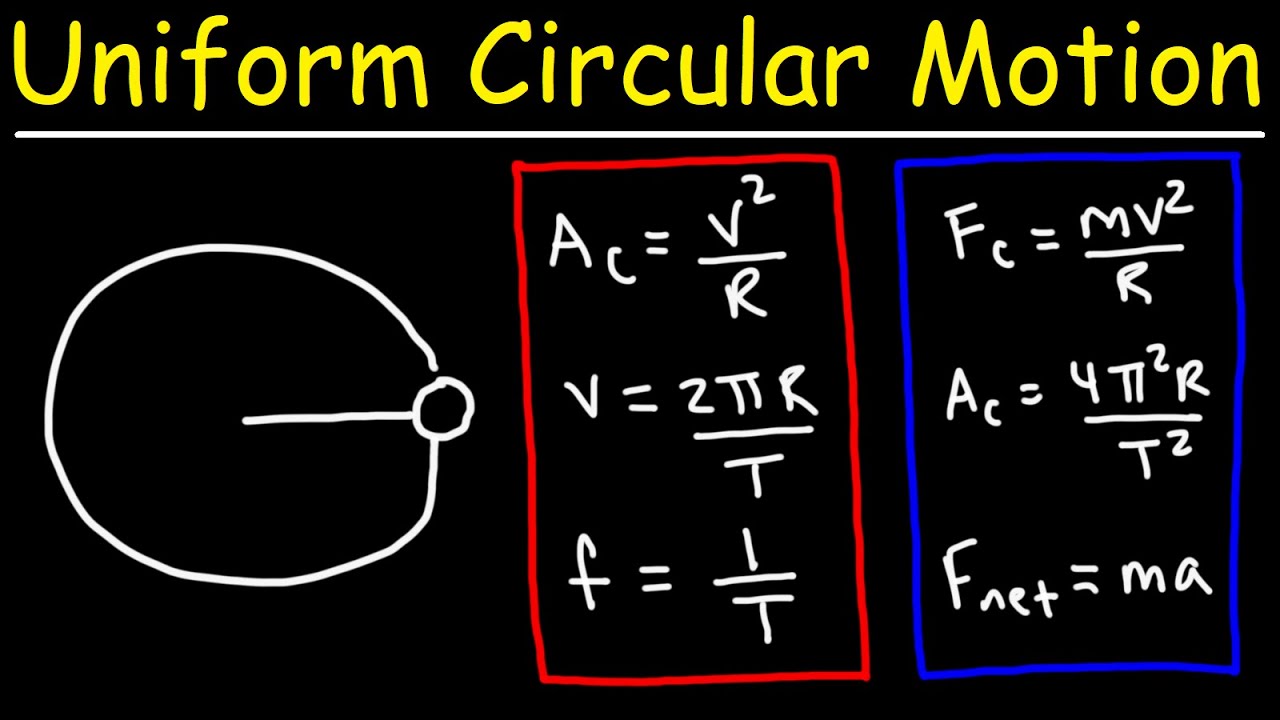
Uniform Circular Motion Formulas and Equations - College Physics
AP Physics 1 - Unit 1 Summary - Kinematics

Center of Mass - AP Physics 1: Unit 2 Review Supplement

Every Physics Law Explained in 11 Minutes
5.0 / 5 (0 votes)