Exam questions Grade 10 Trigonometry
Summary
TLDRThis educational video explains how to analyze a right triangle using the coordinates of its vertices. The instructor emphasizes the importance of orienting towards the x-axis when constructing the triangle and demonstrates the use of Pythagorean theorem to find the hypotenuse. The video further covers trigonometric functions, specifically sine and cosine, using the triangle's dimensions. It concludes with a calculation involving cosine and cotangent, illustrating how to manipulate trigonometric expressions to arrive at a final result. This clear and methodical approach aids learners in understanding basic trigonometry concepts.
Takeaways
- 😀 Always draw triangles towards the x-axis when plotting coordinates.
- 😀 Understanding coordinates: a point like (-4, -3) means moving 4 units left and 3 units down.
- 😀 The lengths of triangle sides are always positive; for example, the hypotenuse calculated is 5.
- 😀 Use the soccer tour method for trigonometric functions: sin, cos, and tan.
- 😀 For sin(θ), the formula is sin(θ) = opposite/hypotenuse, using -3 as the opposite and 5 as the hypotenuse.
- 😀 The angle 90 - θ can be derived from the triangle's angles, facilitating the use of cos and sin.
- 😀 For cos(90 - θ), you treat the triangle from the perspective of the complementary angle.
- 😀 Cotangent (cot) is the reciprocal of tangent; if tan(θ) = opposite/adjacent, then cot(θ) = adjacent/opposite.
- 😀 When calculating trigonometric values, be mindful of the signs based on the angle's quadrant.
- 😀 Simplifying expressions can lead to straightforward results, as demonstrated with the final calculation of 1.
Q & A
What is the importance of moving towards the x-axis when drawing the triangle?
-Moving towards the x-axis ensures that the triangle is correctly positioned in relation to the coordinate system, allowing for accurate calculations of its sides.
How is the coordinate (-4, -3) interpreted in terms of movement on a graph?
-The coordinate (-4, -3) indicates moving 4 units to the left along the x-axis and 3 units down along the y-axis.
What method is suggested for finding the length of the hypotenuse in a right triangle?
-The Pythagorean theorem is used, where the length of the hypotenuse is found by calculating the square root of the sum of the squares of the other two sides.
What does sin(theta) represent in the context of the triangle described?
-In the triangle, sin(theta) represents the ratio of the length of the opposite side to the hypotenuse, which is -3/5.
What does the expression 'cos(90 - theta)' signify in trigonometry?
-The expression 'cos(90 - theta)' represents the cosine of the complementary angle to theta, which can be related to the sine function.
What is the value of cot(theta) based on the given triangle?
-Cot(theta) is calculated as the ratio of the adjacent side to the opposite side, resulting in -4/-3, which simplifies to 4/3.
How can the value of 5 cos(90 - theta) be simplified?
-5 cos(90 - theta) simplifies to 5 times the sine of theta, which in this case results in -3.
Why is the hypotenuse always considered a positive length?
-The hypotenuse represents a distance, and distances are always expressed as positive values in mathematics.
What is the significance of using the reference angle in trigonometric functions?
-Using the reference angle helps to simplify calculations by relating the trigonometric functions to known ratios, making it easier to find values for sine, cosine, and tangent.
What final result is obtained after calculating 5 cos(90 - theta) + 3 cot(theta)?
-After performing the calculations, the result is 1.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
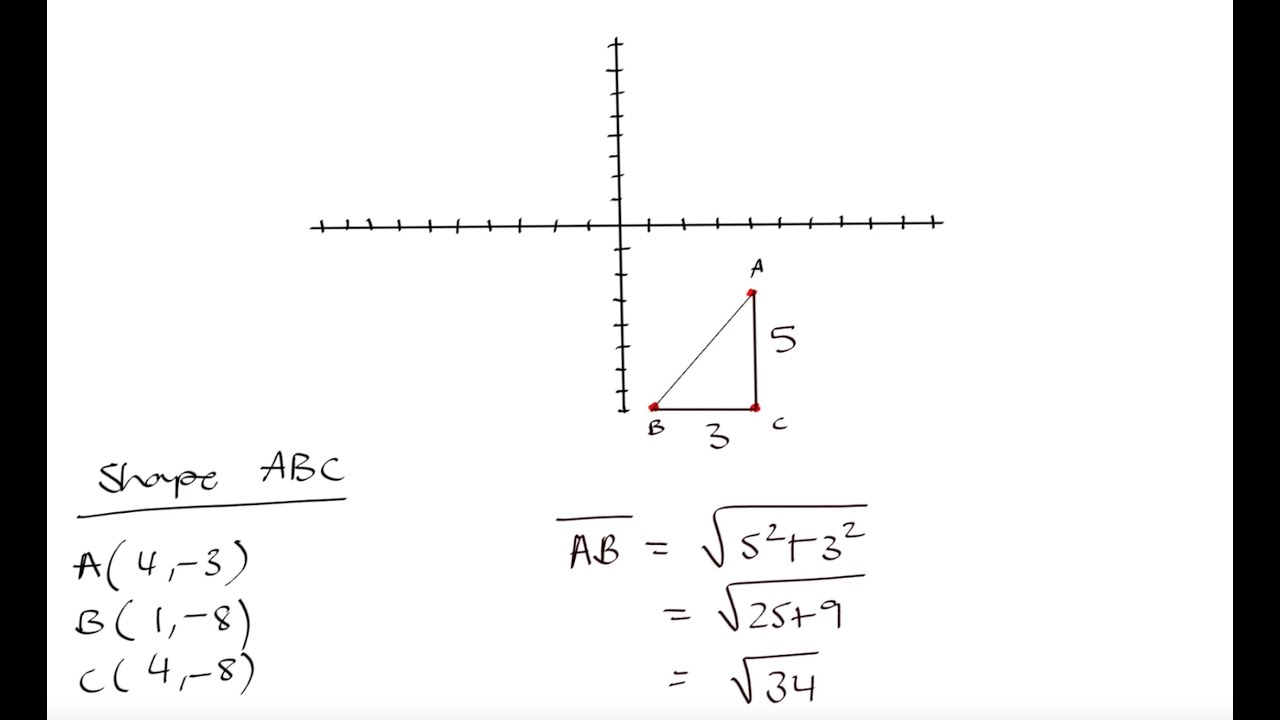
Grade 10 Math: Drawing geometric figures on a Cartesian plane
LINGKARAN DALAM SEGITIGA DAN LINGKARAN LUAR SEGITIGA

LINGKARAN DALAM | LINGKARAN LUAR SEGITIGA | 8 SMP.
DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA

Procedural Generation Tutorial 1 - Planes
Lingkaran Dalam Segitiga - Matematika SMA Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)