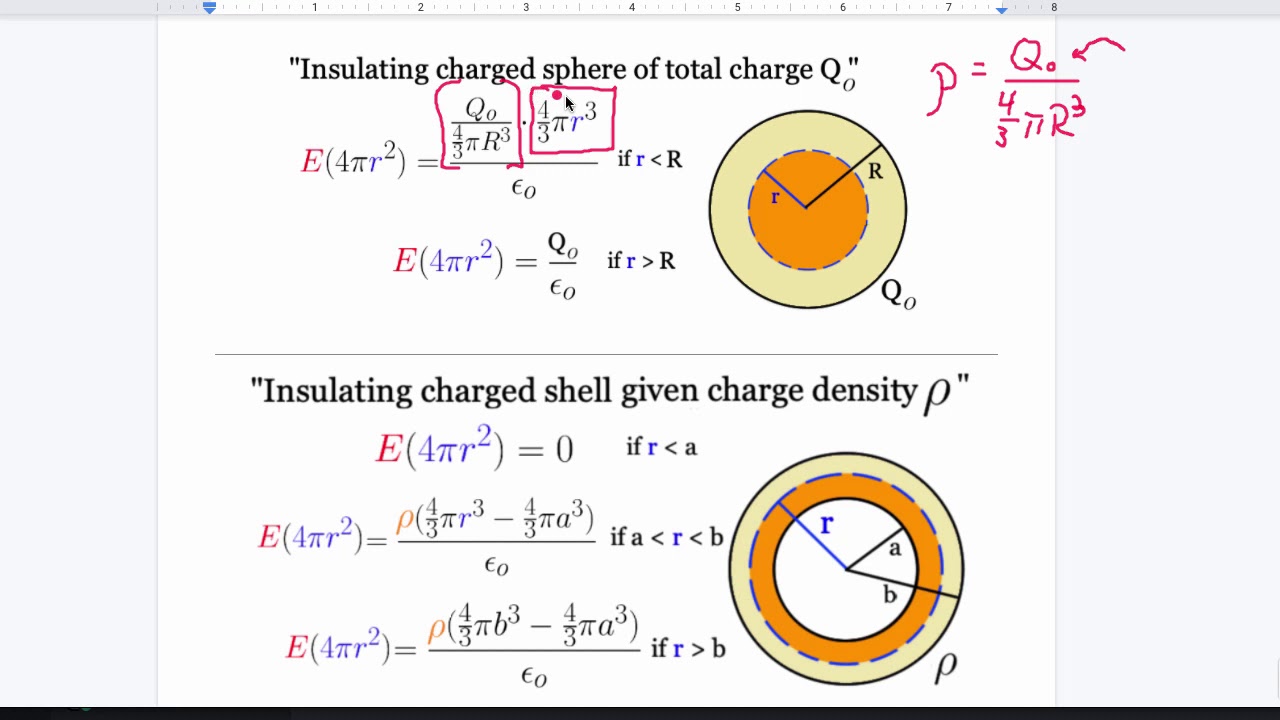CHAMP ET POTENTIEL ÉLECTROSTATIQUES
Summary
TLDRThe video explores the fundamentals of electrostatics, focusing on electric fields generated by charge distributions. It introduces Poisson's equation, which connects electric potential to charge density, and explains how to calculate the potential and electric field at a point. The discussion includes formulas for point charges and illustrates the forces experienced by charges in electric fields, emphasizing the nature of attraction and repulsion based on charge signs. This comprehensive overview of electrostatics combines mathematical concepts with practical examples to enhance understanding of electric interactions.
Takeaways
- 😀 Electrostatics studies electric fields generated by charge distributions.
- 😀 The primary equation used in electrostatics is the divergence of the electric field equation: ∇²E = ρ/ε₀.
- 😀 The equation is related to the electrostatic potential and leads to Poisson's equation: ∇²V = -ρ/ε₀.
- 😀 The potential at a point due to a charge distribution can be calculated using the formula: V_m = (1/4πε₀) ∫(ρ/r) dV.
- 😀 'ρ' represents charge density, and 'r' is the distance from the charge to the point where the potential is being calculated.
- 😀 The electric field 'E' can be derived from the potential using the gradient: E = -∇V.
- 😀 For point charges, the potential is given by V = kQ/r, where 'k' is a constant and 'Q' is the charge.
- 😀 The electric field due to a point charge is expressed as E = kQ/r², directed from the charge towards the observation point.
- 😀 When a charge is placed in an existing electric field, it experiences a force given by F = qE.
- 😀 Coulomb's Law describes the force between two point charges and indicates that like charges repel while opposite charges attract.
Q & A
What is electrostatics?
-Electrostatics is the study of electric fields generated by static charge distributions.
What is the main equation used in electrostatics?
-The primary equation is the divergence of the electric field, expressed as \( \nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0} \), where \( \rho \) is the charge density and \( \epsilon_0 \) is the permittivity of free space.
What is Poisson's equation?
-Poisson's equation is given by \( \nabla^2 V = -\frac{\rho}{\epsilon_0} \) and relates the electric potential \( V \) to the charge density in a given volume.
How is electric potential calculated for a charge distribution?
-The electric potential at a point \( M \) is calculated using the formula \( V(M) = \frac{1}{4\pi\epsilon_0} \int_V \frac{\rho \, dV'}{r} \), where \( r \) is the distance from the charge element to point \( M \).
What relationship exists between electric potential and electric field?
-The electric field \( \mathbf{E} \) can be derived from the electric potential \( V \) through the gradient, expressed as \( \mathbf{E} = -\nabla V \).
What is the formula for electric potential due to a point charge?
-The electric potential due to a point charge \( Q \) is given by \( V = \frac{Q}{4\pi\epsilon_0 r} \), where \( r \) is the distance from the charge.
How is the electric field from a point charge expressed mathematically?
-The electric field \( \mathbf{E} \) from a point charge is expressed as \( \mathbf{E} = \frac{Q}{4\pi\epsilon_0 r^2} \hat{u} \), where \( \hat{u} \) is the unit vector pointing from the charge to the observation point.
What force does a charge experience when placed in an electric field?
-A charge \( q' \) placed in an electric field \( \mathbf{E} \) experiences a force given by \( \mathbf{F} = q' \mathbf{E} \).
What is the significance of charge signs in electrostatic interactions?
-The signs of the charges determine the nature of the force: like charges repel each other, while opposite charges attract.
How can symmetry and invariance simplify electric field calculations?
-Using symmetry and invariance in charge distributions allows for simpler formulations of electric fields, which can reduce the complexity of the calculations involved.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)