Routh-Hurwitz Criterion, An Introduction

Summary

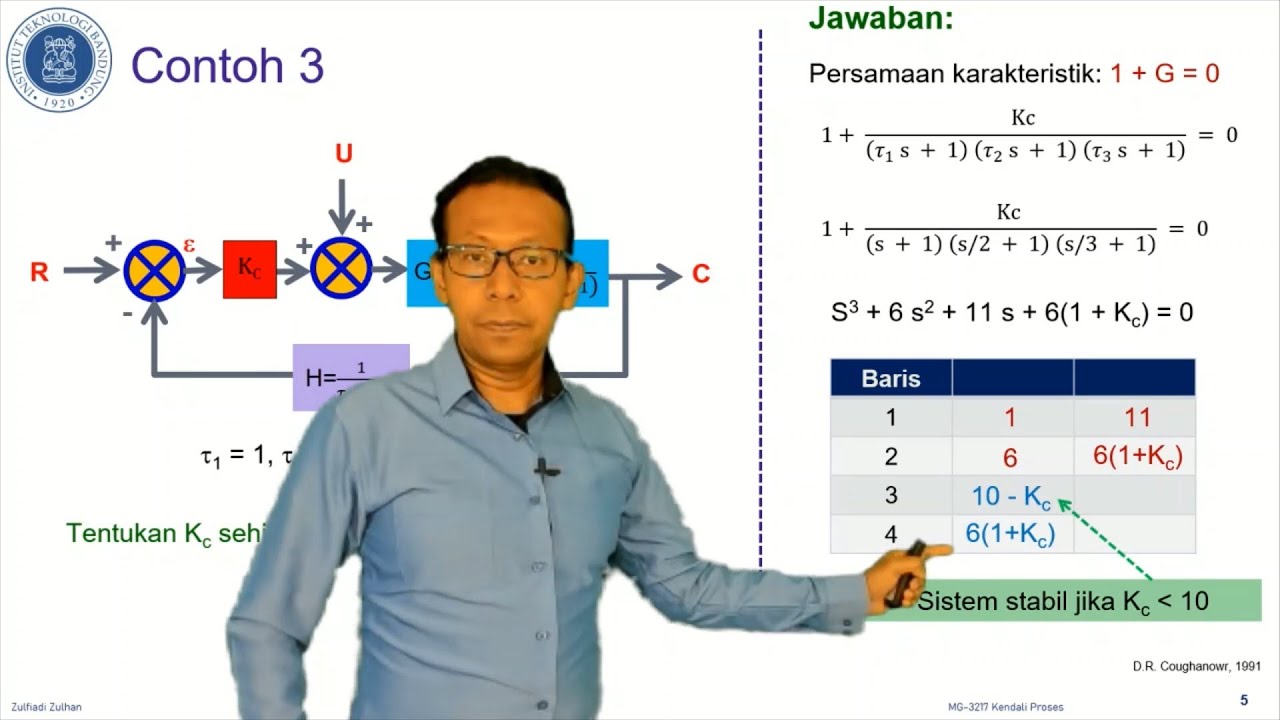
In this lecture on control systems, the Routh-Hurwitz criterion and Routh array are explored as methods for assessing system stability without directly calculating roots. The instructor explains that a system is stable if all roots of the characteristic polynomial lie in the left-half plane. The construction of the Routh array using the polynomial's coefficients is demonstrated, highlighting the significance of sign changes in the first column to determine stability. Through practical examples, the video illustrates how to identify unstable systems, making complex concepts accessible for students of classical control theory.

Takeaways

• 😀 A system is stable if all roots of its characteristic polynomial lie in the left half-plane (negative real parts).
• 😀 The poles of the transfer function correspond to the roots of the characteristic equation.
• 😀 The Routh-Hurwitz criterion provides a method to assess stability without calculating roots directly.
• 😀 A negative coefficient in the characteristic polynomial indicates instability; at least one root lies in the right half-plane.
• 😀 You can have a polynomial with all positive coefficients yet still have an unstable system if it has roots in the right half-plane.
• 😀 The Routh array is structured to assess the stability of higher-order polynomials by analyzing their coefficients.
• 😀 To construct the Routh array, list polynomial coefficients in a descending order of powers of s and fill out using an up-down pattern.
• 😀 Each entry in the Routh array can be calculated using specific multiplication and subtraction rules from previous entries.
• 😀 Counting the number of sign changes in the first column of the Routh array helps determine the number of roots in the right half-plane.
• 😀 The Routh-Hurwitz criterion simplifies the process of stability analysis, especially for complex polynomials, making it accessible for engineers.

Q & A

What is the primary goal of the Routh-Hurwitz criterion?

The primary goal of the Routh-Hurwitz criterion is to determine the stability of a control system by assessing whether all roots of its characteristic polynomial lie in the left-half plane.

How does one identify a stable system using the Routh-Hurwitz criterion?

A system is identified as stable if all the roots of its characteristic polynomial, derived from the transfer function, have negative real parts, meaning they lie in the left-half plane.

What is a characteristic polynomial in the context of control systems?

The characteristic polynomial is the polynomial equation formed by setting the denominator of the transfer function to zero. Its roots correspond to the system's poles.

Can a system with all positive coefficients still be unstable?

Yes, a system can have all positive coefficients in its polynomial and still be unstable if any of its roots lie in the right-half plane.

What does the Routh array help to assess?

The Routh array helps assess the stability of a system by allowing one to determine the signs of the coefficients and their combinations without directly solving for the roots.

What is the significance of sign changes in the first column of the Routh array?

Sign changes in the first column of the Routh array indicate the presence of roots in the right-half plane, thus suggesting that the system is unstable.

What steps are involved in setting up a Routh array?

To set up a Routh array, write the polynomial in descending powers of s, fill the first two rows with coefficients in an up-down pattern, and then use a mathematical pattern to fill out the remaining rows.

What happens if a row in the Routh array contains all zeros?

If a row in the Routh array contains all zeros, it indicates the possibility of a root on the imaginary axis, leading to the need for special handling to determine stability.

What does a negative coefficient in the characteristic equation imply?

A negative coefficient in the characteristic equation implies that there is at least one pole in the right-half plane, which indicates that the system is unstable.

How does the Routh-Hurwitz criterion simplify the analysis of higher-order polynomials?

The Routh-Hurwitz criterion simplifies the analysis of higher-order polynomials by providing a systematic approach to determine stability through the Routh array, avoiding the complexity of calculating all roots.