A Secret Weapon for Predicting Outcomes: The Binomial Distribution
Summary
TLDRThis video explains the binomial distribution through the example of a 60% free throw shooter, illustrating how to calculate the probability of making a specific number of successful shots out of multiple attempts. It uses visual aids, such as blobs and 3D grids, to demonstrate various outcomes and their associated probabilities. The video introduces key concepts like the binomial coefficient, factorials, and the significance of independent events, ultimately culminating in the formula for determining the likelihood of achieving a certain number of successes. It emphasizes the importance of understanding this distribution in the context of repeated yes-or-no scenarios.
Takeaways
- 😀 Effective hospital management systems are crucial for improving patient care and operational efficiency.
- 😀 Implementing a robust data management system can streamline hospital processes and enhance decision-making.
- 😀 Training staff on the use of hospital management systems is essential to maximize their benefits.
- 😀 Integrating various departments through a centralized system can improve communication and reduce errors.
- 😀 Patient engagement tools within management systems can enhance satisfaction and retention rates.
- 😀 Regular updates and maintenance of the management system are necessary to ensure it meets evolving healthcare needs.
- 😀 Data security and patient confidentiality should be prioritized in any hospital management system implementation.
- 😀 Utilizing analytics can help hospitals identify trends and areas for improvement in service delivery.
- 😀 Collaboration with stakeholders is vital for the successful adoption of new management technologies.
- 😀 Continuous feedback from users can guide future enhancements and optimize the management system.
Q & A
What is the primary focus of the video script?
-The video script focuses on explaining the binomial distribution and how to calculate the probability of making a certain number of successful shots, specifically in the context of free throw shooting.
What does the term 'binomial' signify in this context?
-The term 'binomial' refers to situations with two possible outcomes, such as success or failure, which allows the results to be categorized into two groups.
How do you calculate the probability of a specific outcome in the binomial distribution?
-The probability is calculated using the binomial formula, which involves multiplying the number of ways to achieve a specific outcome (binomial coefficient) by the probabilities of success and failure raised to their respective powers.
What is the binomial coefficient and why is it important?
-The binomial coefficient represents the number of ways to arrange a certain number of successes in a set number of trials. It is crucial for calculating the overall probability of achieving a specific number of successes.
What does Pascal's Triangle have to do with the binomial distribution?
-Pascal's Triangle provides a visual representation of the binomial coefficients, helping to determine the number of ways to achieve different numbers of successes in a series of trials.
What is the formula for the binomial coefficient?
-The formula for the binomial coefficient is given by n! / (k! * (n - k)!), where n is the total number of trials, k is the number of successes, and '!' denotes factorial.
What assumptions must be made when using the binomial distribution?
-One key assumption is that the trials are independent, meaning the outcome of one trial does not affect the outcome of another.
Can the binomial distribution be applied to other situations beyond free throw shooting?
-Yes, the binomial distribution applies to any scenario where there are repeated trials with two possible outcomes, such as coin tosses or quality control in manufacturing.
How does the video suggest verifying the binomial distribution calculations?
-The video suggests verifying the calculations by testing the formula against randomized results or simulations, like running trials with a large number of attempts to compare theoretical probabilities with observed outcomes.
Why is it important to understand both the structure and the practical application of the binomial distribution?
-Understanding both the structure and practical applications allows for better statistical analysis in real-world situations, enabling more accurate predictions and decisions based on probabilistic outcomes.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

0625 Distribución binomial negativa

Distribusi Binomial • Part 6: Contoh Soal Distribusi Peluang Variabel Acak Diskrit (3)

Kelas XII / Distribusi Peluang Binomial

Finding The Probability of a Binomial Distribution Plus Mean & Standard Deviation

Distribusi Probabilitas Binomial | Matematika Peminatan Kelas 12
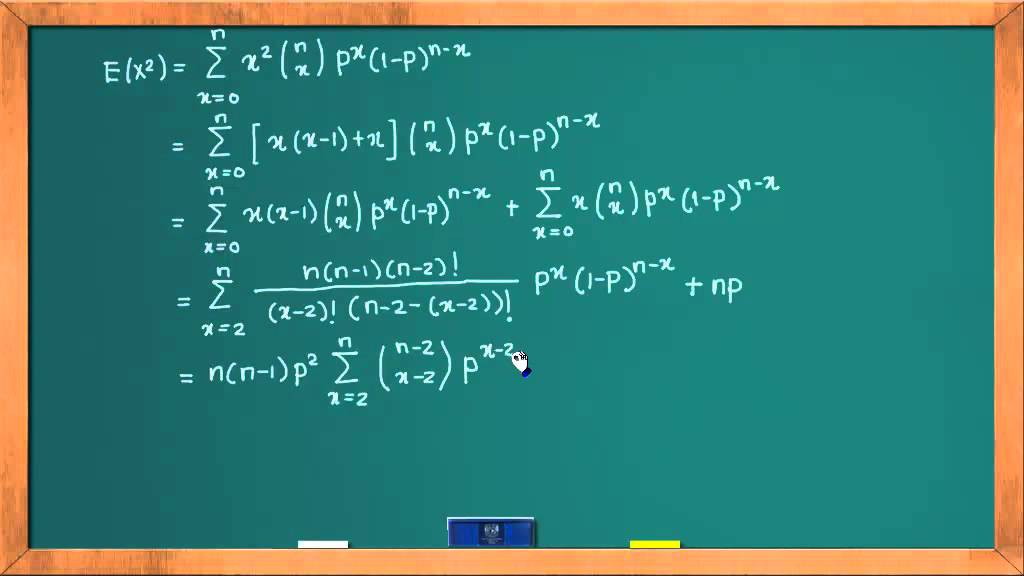
0625 Distribución binomial
5.0 / 5 (0 votes)