Physik LF / Video B13: Spiralbahn

Summary

This video script explains the motion of charged particles in magnetic fields, focusing on how particles describe spiral paths when shot at an angle to the field lines. The lecturer describes the decomposition of velocity into components, one parallel and one perpendicular to the magnetic field, and how this influences the particle's trajectory. The spiral motion is derived from Lorentz force and the resulting equations, with a focus on calculating key parameters such as the radius and pitch of the spiral. The approach uses a combination of kinematic principles and magnetic field equations to model the behavior of electrons in the field.

Takeaways

• 😀 The script discusses the motion of charged particles in magnetic fields, particularly how they describe a spiral path.
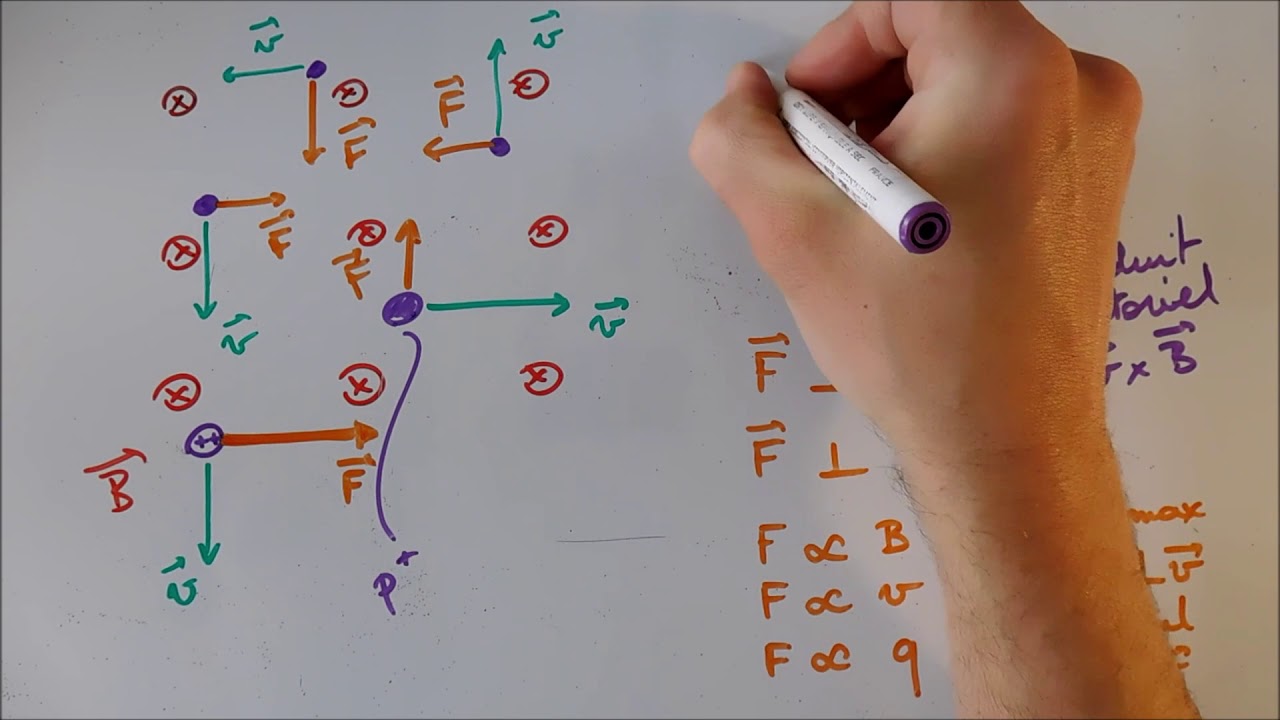
• 😀 The spiral path occurs when particles are not shot perpendicular to the magnetic field lines, but at an angle α that is neither parallel nor perpendicular.
• 😀 The velocity vector is broken down into two components: one parallel to the magnetic field (v parallel) and one perpendicular to it (v perpendicular).
• 😀 The component of velocity parallel to the field does not experience any Lorentz force, and thus it does not affect the particle's trajectory.
• 😀 The perpendicular component causes the particle to follow a circular motion, as it experiences the Lorentz force that changes its direction.
• 😀 The resulting motion combines both circular and linear components, leading to a spiral trajectory for the charged particle.
• 😀 The particle is essentially carried upwards in a spiral as it moves around the circular path, resembling a helical or spiral staircase.
• 😀 The radius of the spiral path is determined by the perpendicular velocity component, and the characteristic height between loops is known as the 'gang height' of the spiral.
• 😀 The Lorentz force is key in dictating the circular part of the motion, while the parallel component of velocity leads to the upward motion.
• 😀 The spiral's radius can be calculated using the formula radius = mv perpendicular / (qB), where q is the charge, B is the magnetic field strength, and v perpendicular is the perpendicular velocity component.
• 😀 The time it takes for the particle to complete one loop in the spiral can be derived, and the gang height of the spiral is determined by the time it takes for the particle to move upwards by a certain distance.

Q & A

What happens when charged particles move in a magnetic field?

When charged particles like electrons move in a magnetic field, they experience a force known as the Lorentz force, which causes them to move in a circular or spiral path, depending on the angle at which they enter the field.

What type of motion do the electrons exhibit in the experiment described in the transcript?

In the experiment, electrons exhibit spiral motion, which is a result of the combination of their perpendicular and parallel components of velocity relative to the magnetic field.

What is the significance of the angle at which particles enter the magnetic field?

The angle at which particles enter the magnetic field affects the trajectory. If the angle is neither parallel nor perpendicular to the magnetic field lines, the resulting motion will be a spiral, as the velocity can be broken into components.

What role does the Lorentz force play in the motion of charged particles in a magnetic field?

The Lorentz force acts perpendicular to both the velocity of the charged particles and the magnetic field, causing the particles to follow a curved path. When the velocity component is parallel to the field, this force is absent, and only the perpendicular component contributes to the motion.

What are the two components of the velocity vector that affect the electron's motion in the field?

The velocity vector is split into two components: one parallel to the magnetic field lines and the other perpendicular to them. The parallel component does not contribute to the Lorentz force, while the perpendicular component causes circular motion.

How does the speed of the electron relate to the radius of its spiral path?

The radius of the spiral path is determined by the perpendicular component of the electron's velocity and the strength of the magnetic field. The greater the perpendicular velocity, the larger the radius of the spiral.

What is the role of the tangential velocity in the spiral motion?

The tangential velocity, shown by the yellow arrow in the diagram, is always tangent to the curve of the spiral, and its magnitude corresponds to the motion of the electron along the circular path. This component dictates the electron's circular motion.

How can the radius of the spiral path be calculated?

The radius of the spiral path can be calculated by using the formula: radius = (m * v_perpendicular) / (q * B), where m is the mass of the electron, v_perpendicular is the perpendicular velocity component, q is the charge of the electron, and B is the magnetic field strength.

What is meant by the 'gang height' of the spiral path?

The 'gang height' refers to the vertical distance between two points where the electron has the same speed. It is effectively the step height of the electron's spiral motion as it progresses through the magnetic field.

How can the period of the electron's motion along the spiral path be determined?

The period of the electron's motion can be determined by considering the time it takes for the electron to complete one circular orbit. This is based on the electron's parallel velocity and the radius of the circular motion, and the time is proportional to the mass of the electron and the strength of the magnetic field.