Friedman Test [Simply Explained]

Summary

The video explains the Friedman test, a non-parametric method for analyzing differences among three or more dependent samples. It contrasts this test with the analysis of variance with repeated measures, highlighting that the Friedman test uses ranks instead of actual values, making it suitable for non-normally distributed data. The video presents a practical example involving pain perception during therapy, emphasizing the importance of hypotheses in the Friedman test. Additionally, it demonstrates how to perform the test using a software tool and by hand, providing insights into calculations and interpretations of results.

Takeaways

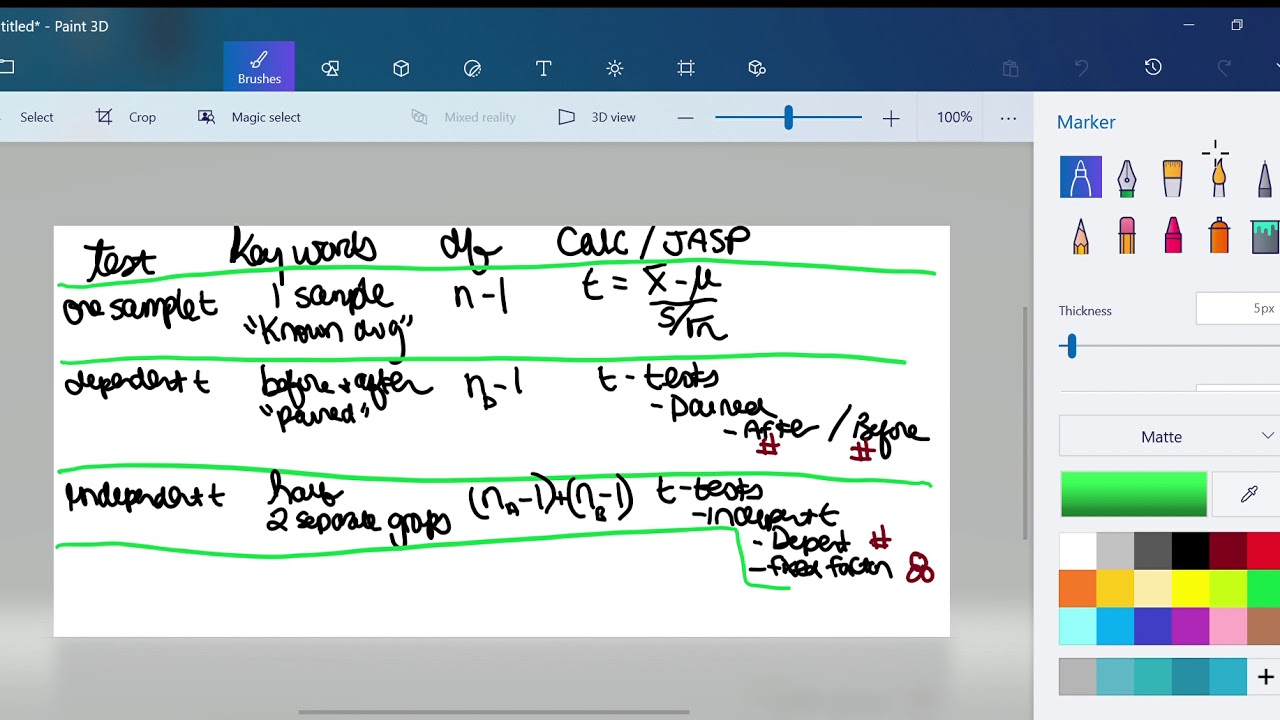
• 😀 The Friedman test is used to analyze statistically significant differences among three or more dependent samples.
• 😀 A dependent sample involves repeated measurements from the same subjects, such as pre- and post-treatment evaluations.
• 😀 The Friedman test is the non-parametric equivalent of repeated measures ANOVA, analyzing ranks instead of raw data values.
• 😀 Ranks are assigned based on the measured values, allowing the Friedman test to work without the assumption of normal distribution.
• 😀 The main research question addressed by the Friedman test is whether there are significant differences between more than two dependent groups.
• 😀 An example in the video assesses the impact of therapy on patients' pain perception at different times during treatment.
• 😀 The null hypothesis of the Friedman test states that there are no significant differences between the dependent groups.
• 😀 The alternative hypothesis posits that at least one group shows a significant difference from the others.
• 😀 The video provides a step-by-step guide on how to perform the Friedman test using both software (DataTab) and manual calculations.
• 😀 The results include a p-value, which helps determine whether to reject or retain the null hypothesis based on a chosen significance level.

Q & A

What is the Friedman test used for?

The Friedman test analyzes whether there are statistically significant differences between three or more dependent samples.

What defines a dependent sample?

A dependent sample consists of measured values that are linked, such as data collected from the same individuals at different time points.

How does the Friedman test differ from ANOVA with repeated measures?

While both tests assess differences between dependent groups, the Friedman test uses ranks of the measured values instead of the actual values, making it a non-parametric test.

Why are ranks used in the Friedman test?

Ranks are used to allow the test to be applicable even when the data are not normally distributed, thus accommodating non-parametric data.

What is the null hypothesis in the context of the Friedman test?

The null hypothesis states that there are no significant differences between the dependent groups.

What statistical outcome does the Friedman test provide?

The Friedman test calculates a chi-square statistic, which is then compared to a critical value to determine whether to reject the null hypothesis.

How is the chi-square value calculated in the Friedman test?

The chi-square value is calculated using a specific formula that incorporates the sum of ranks for each group and the number of subjects.

What is the significance level commonly used in the Friedman test?

A common significance level used in the Friedman test is 0.05.

What should be done if the p-value is greater than the significance level?

If the p-value is greater than the significance level, the null hypothesis is retained, indicating no significant differences among the groups.

Can you explain a practical example of the Friedman test?

A practical example would be measuring pain perception in patients undergoing therapy at different times to see if therapy impacts pain levels over time.