Two Sample t-test for Independent Groups | Statistics Tutorial #23| MarinStatsLectures
Summary
TLDRThis video introduces the independent two-sample t-test, a statistical method used to compare the means of two independent groups. It discusses key features, including assumptions about the groups' variances and the importance of independent samples. Using an example comparing sleep hours between individuals with and without brain injuries, it illustrates how to calculate the difference in means, standard error, and p-values. The video emphasizes the significance of hypothesis testing and confidence intervals, ultimately guiding viewers through interpreting statistical results in a meaningful context.
Takeaways
- 😀 Independent two-sample t-tests compare the means of two independent groups with a categorical X variable and a numeric Y variable.
- 😀 One advantage of independent groups is the simplicity in calculations, as there's no need to consider relationships between groups.
- 😀 A drawback of independent groups is that differences in other characteristics (e.g., age, gender) may confound results.
- 😀 Pairing can help control for these confounding factors, but it's not possible in all situations (e.g., brain injury studies).
- 😀 The example discussed compares sleep hours between individuals with and without a brain injury.
- 😀 Summary statistics indicate that the brain injury group sleeps, on average, 0.7 hours more than the non-injury group.
- 😀 Standard error is crucial for understanding how much sample estimates may vary from the true population mean difference.
- 😀 Two assumptions are made when calculating standard error: equal or unequal population standard deviations between groups.
- 😀 A null hypothesis of no difference in means is tested against an alternative hypothesis using sample data.
- 😀 A p-value of 0.006 indicates strong evidence against the null hypothesis, suggesting a statistically significant difference in sleep hours.
Q & A
What is an independent two-sample t-test used for?
-An independent two-sample t-test is used to compare the means of two independent groups, typically with one categorical variable (X) with two levels and one numeric variable (Y).
What are some advantages of using independent groups for comparison?
-One advantage is the mathematical simplicity; the groups do not need to have any relationship or dependency. This makes calculations more straightforward.
What is a potential disadvantage of comparing independent groups?
-A disadvantage is that the groups may differ in ways other than just the treatment or characteristic being studied, which can introduce confounding variables.
How can we control for confounding variables when comparing independent groups?
-We can match individuals in the two groups on certain characteristics or use random assignment to treatments. Multivariable methods can also be used to adjust for these differences.
What is the formula for calculating the difference in means?
-The difference in means is calculated as the mean for Group 1 minus the mean for Group 2.
What does the standard error of the estimate tell us?
-The standard error of the estimate indicates how far, on average, the sample difference in means is expected to move from the true population mean difference.
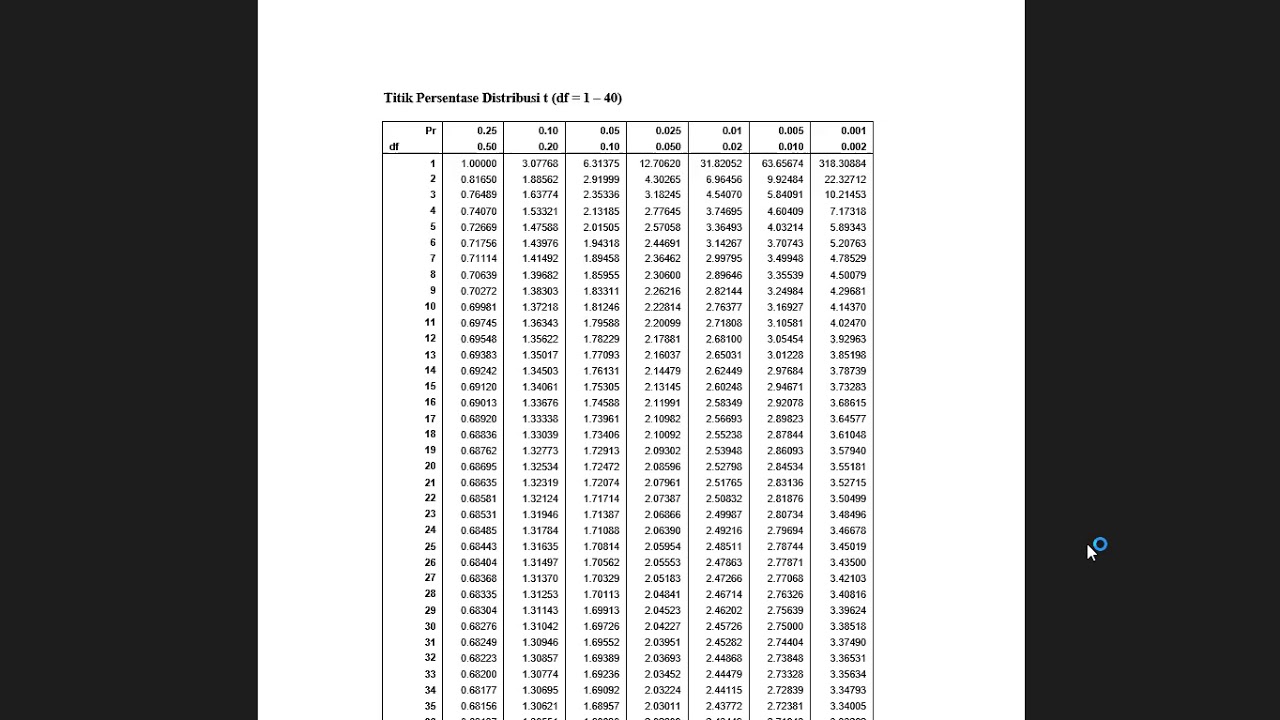
What assumptions must be met for the independent two-sample t-test?
-Assumptions include having a simple random sample, independent observations, sufficiently large sample sizes (typically larger than 20), and that each group's distribution should be approximately normal.
What is the null hypothesis in this context?
-The null hypothesis states that the difference in means between the two groups is zero, indicating no effect or difference at the population level.
How is the p-value interpreted in the context of hypothesis testing?
-The p-value indicates the probability of observing a sample difference as extreme as the one found, assuming the null hypothesis is true. A low p-value suggests rejecting the null hypothesis.
What is a confidence interval, and how does it relate to hypothesis testing?
-A confidence interval provides a range of values within which we can be confident that the true population parameter lies. If the interval does not include zero, it supports rejecting the null hypothesis.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)