Mekanika Fluida #9 - Centre of buoyancy
Summary
TLDRIn this educational video, the instructor discusses the concept of buoyancy, focusing on the center of buoyancy and its relationship to fluid mechanics. Using practical examples, such as a wooden block floating in water, the video explains how to calculate the volume of displaced water and the depth of submerged objects. Additionally, it examines scenarios involving a concrete block placed on top of a wooden block and explores the effects of different densities in fluids, such as mercury and water. The instructor emphasizes understanding buoyancy principles through engaging problem-solving to enhance students' comprehension.
Takeaways
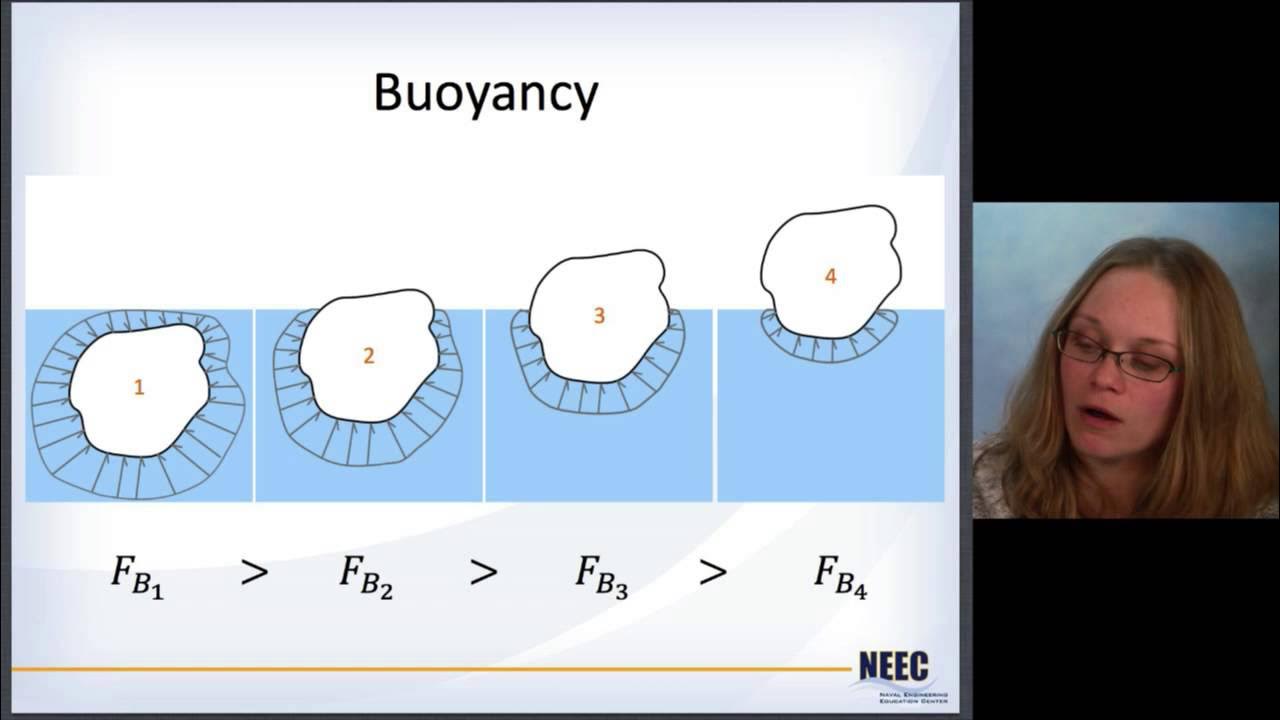
- 😀 The center of buoyancy is the point where the buoyant force acts, aligning with the center of mass of the displaced fluid.
- 📏 Buoyant force is equal to the weight of the fluid displaced by a submerged object, following Archimedes' principle.
- 🌊 Understanding the center of pressure is crucial for analyzing forces acting on submerged surfaces.
- 📐 Example 1 demonstrates the calculations of buoyancy for a wooden block with specific dimensions floating in water.
- 🔍 In Example 1, the volume of water displaced is calculated to find the depth of submersion (H).
- 🔗 The relationship between the weight of the object and the buoyant force is key for equilibrium in floating bodies.
- 🪨 Example 2 discusses a wooden block with a concrete block placed on top, analyzing different submersion scenarios.
- ⚖️ In Example 2, calculations show how total weight must equal the buoyant force for both blocks to float properly.
- 🔬 Example 3 involves a metal object submerged in both water and mercury, illustrating buoyancy in different fluids.
- 📚 The lecture encourages further study with additional examples to strengthen understanding of buoyancy concepts.
Q & A
What is the main topic discussed in this video?
-The video focuses on the concept of buoyancy, particularly the center of buoyancy, and its relation to the principles of Archimedes.
What is the center of buoyancy?
-The center of buoyancy is the point where the buoyant force acts, which corresponds to the center of mass of the fluid displaced by an object submerged in a fluid.
How is the volume of an object related to its buoyancy?
-The volume of an object submerged in a fluid determines the volume of fluid displaced, which directly affects the buoyant force acting on the object.
In the first example, what dimensions are given for the wooden block?
-The wooden block has a width of 1.25 meters, a depth of 0.75 meters, and a length of 3 meters.
How is the weight of the wooden block calculated?
-The weight of the wooden block is calculated by multiplying its specific gravity (6.4) by its volume (1.25 * 0.75 * 3), resulting in a weight of 18 kN.
What determines the position of the center of buoyancy for a submerged object?
-The position of the center of buoyancy is always at the center of mass of the volume of fluid displaced by the submerged part of the object.
What happens when the wooden block is submerged completely?
-When the wooden block is completely submerged, the center of buoyancy coincides with the center of mass of the block.
What is the significance of the depth of the submerged object?
-The depth of the submerged object influences the buoyant force, as greater depth results in a larger volume of fluid being displaced, thus increasing the buoyant force.
In the second example, what is the specific gravity of the concrete placed on the wooden block?
-The specific gravity of the concrete is given as 2.5.
How does the presence of concrete affect the buoyancy of the wooden block?
-The addition of concrete increases the total weight acting on the wooden block, affecting the balance of forces and potentially leading to the block being submerged entirely, depending on the weight of the concrete.
What two fluids are mentioned in the final problem involving the metal object?
-The two fluids mentioned are water and mercury.
How is the weight of the metal object determined in the last example?
-The weight of the metal object is determined by balancing the upward buoyant forces from both fluids with the weight of the object, leading to the conclusion that the weight is 53.7.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)