Logarithms in the Real World
Summary
TLDRThis video delves into the significance of logarithms in the real world, highlighting their historical use in simplifying calculations before calculators and computers. It illustrates how logarithms help us understand vast ranges of measurements, from light intensity and sound levels to earthquake magnitudes and acidity in solutions. Through practical examples like the Richter scale and the pH scale, the video emphasizes the logarithmic nature of these phenomena. Ultimately, it showcases how logarithms remain essential in various scientific fields, providing a foundation for comprehending complex data and measurements.
Takeaways
- 😀 The use of logarithms has decreased in the past 30 years due to the prevalence of calculators and computers.
- 📚 Logarithms were historically essential for multiplication and division, often presented in tables in textbooks and scientific journals.
- 🚀 Logarithms were used in slide rules, which were critical tools for calculations during space missions, including the moon landing.
- 🌌 Logarithmic scales help manage and understand extremely large numbers, particularly in scientific measurements.
- 💡 Human sensitivity to light operates on a logarithmic scale, impacting how we perceive brightness and adjust to varying light levels.
- 🌍 The Richter scale for measuring earthquakes is logarithmic, meaning a higher magnitude corresponds to a significantly increased shaking amplitude.
- 🔬 Acidity levels are determined using a logarithmic function, represented in pH levels based on hydrogen ion concentration.
- 🎧 Sound intensity is measured in decibels, where each 10 dB increase represents a tenfold increase in sound intensity.
- 🌟 The brightness of stars is categorized by a logarithmic magnitude scale, where a decrease in magnitude indicates a brighter light source.
- ⏳ Logarithmic functions are utilized in radioactive dating to calculate ages based on exponential changes in quantities.
Q & A
How has the use of logarithms changed in the past 30 years?
-The active use of logarithms has decreased due to the widespread availability and use of calculators and computers, which have replaced the need for logarithmic tables in textbooks and scientific journals.
What is the primary value of logarithms today?
-Logarithms are used to create a shorthand or code to make extremely large numbers more manageable and understandable, especially in scientific measurements.
How do logarithms relate to human vision?
-Human sensitivity to light is logarithmic, meaning that our perception of light intensity can adjust across a wide range of levels, allowing us to perceive vastly different light inputs.
What is the Richter scale, and how does it use logarithms?
-The Richter scale measures the intensity of earthquakes using a base 10 logarithmic scale, where a 5.0 earthquake has twice the shaking amplitude of a 4.0 earthquake.
How is pH related to logarithms?
-pH is determined by a logarithmic function that relates the concentration of hydrogen ions in a solution; a lower pH indicates a higher concentration of hydrogen ions.
What is the relationship between decibels and logarithms?
-Decibels measure sound intensity using a base 10 logarithmic scale, where each increase of 10 decibels corresponds to a tenfold increase in sound intensity.
How does the magnitude scale for stars use logarithms?
-The magnitude scale classifies light intensity logarithmically; a light source with a 0 magnitude is 100 times more intense than one with a 5 magnitude, with each step representing a factor of approximately 2.5 increase in brightness.
What is an 'order of magnitude'?
-An order of magnitude refers to an exponential change of plus or minus 1 in the value of a quantity, typically used in relation to powers of 10; for example, 1000 is one order of magnitude greater than 100.
What is the common logarithm?
-The common logarithm, or log base 10, is used due to humans having 10 counting digits, making it a natural choice for our number system.
How can you calculate the common logarithm using a calculator?
-To calculate the common logarithm of a number, press the 'log' key on a graphing calculator, enter the number, and then press 'Enter' to obtain the result.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Origem Histórica dos Logaritmos: de onde vem os logaritmos?
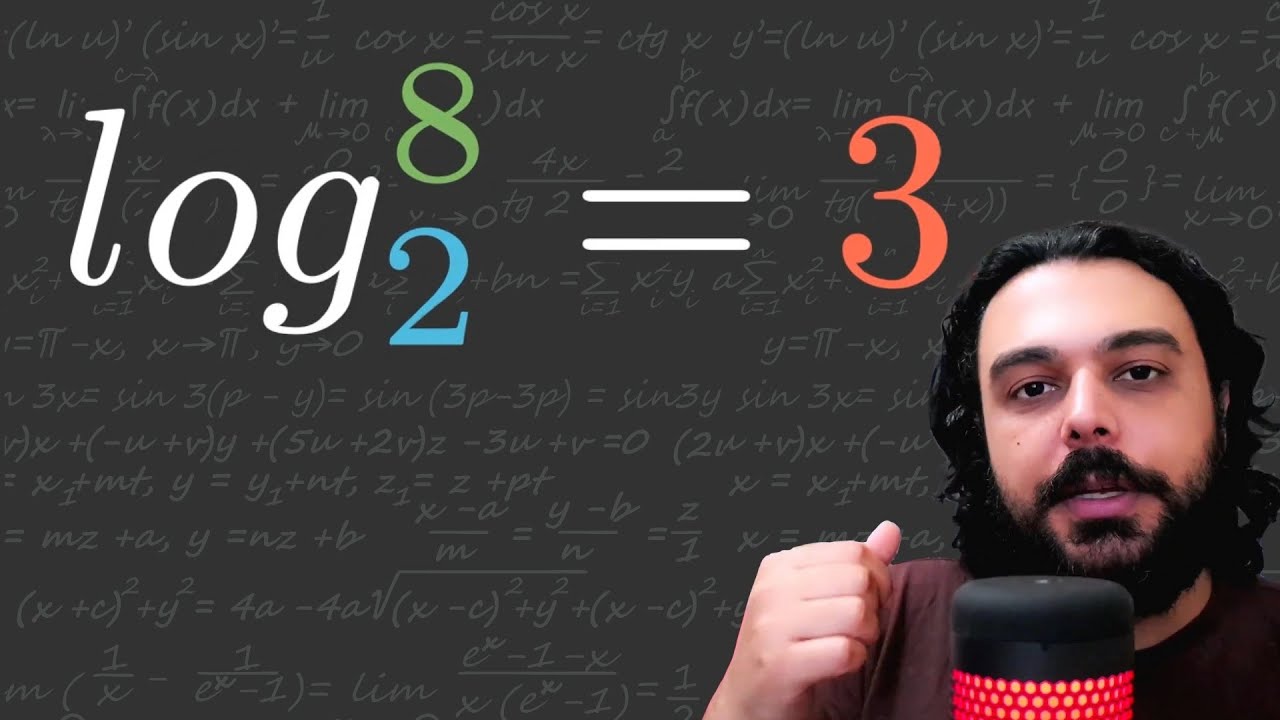
Para que servem os LOGARITMOS?

LOGARITMA ITU GAMPANG!! Bahas Logaritma Kelas 10 | Study With Jerome Polin

Matemática - Aula 13 - Logaritmo - Parte 1

Os COMPUTADORES eram PESSOAS! #SagaDosComputadores Ep.1

Logarithms - What is e? | Euler's Number Explained | Infinity Learn NEET
5.0 / 5 (0 votes)