Simpson's Rule & Numerical Integration

Summary

In this instructional video, Simpson's Rule is explained as a method for estimating definite integrals, specifically through a practical example involving the integral of x³ from 2 to 10. The video illustrates the calculation of delta x, application of the formula, and comparison of Simpson's estimate with the exact integral value. Additionally, it applies Simpson's Rule to calculate the displacement of a car over 30 minutes using a provided velocity table, leading to the determination of average speed. The close comparison of results emphasizes the reliability of the approximation method for evaluating areas under curves.

Takeaways

• 😀 Simpson's Rule is a method for estimating the value of definite integrals using a specific formula that involves evaluating a function at several points.
• 📏 The width of each subinterval, denoted as Δx, is calculated as (b - a) / n, where 'a' and 'b' are the limits of integration and 'n' is the number of intervals.
• 🔢 For the given example, with a = 2, b = 10, and n = 4, Δx is determined to be 2.
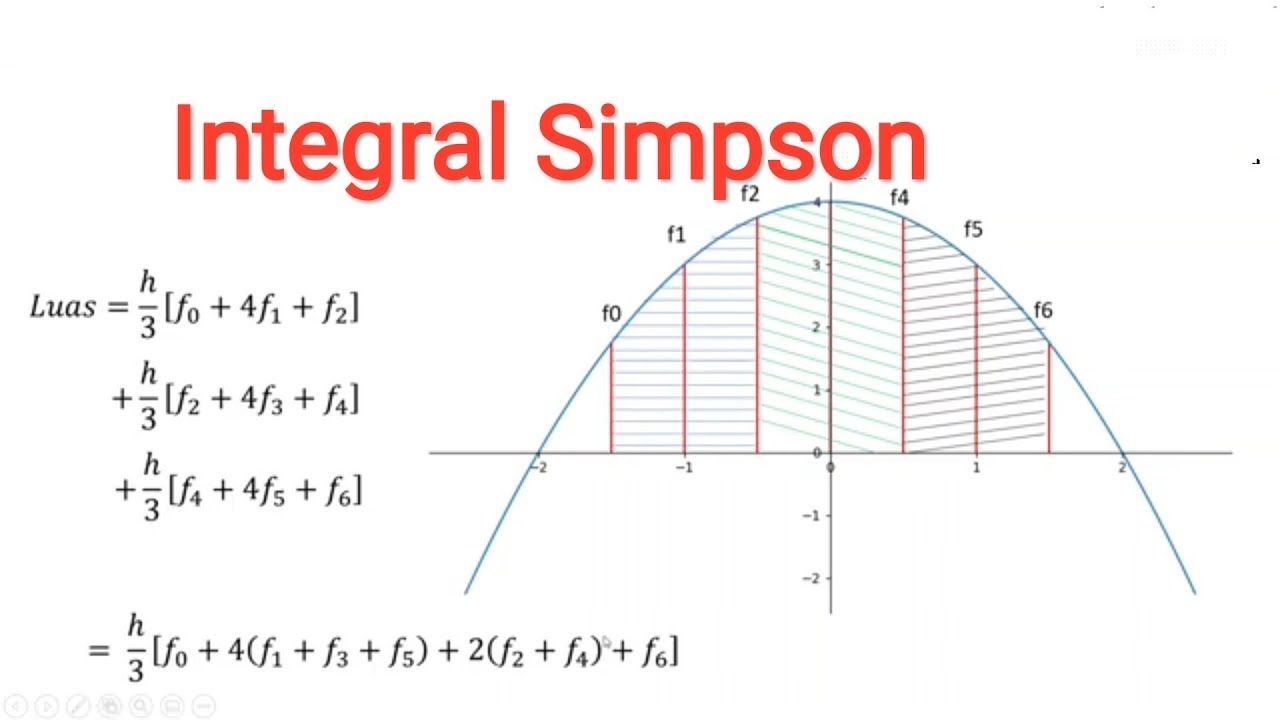
• 📊 In Simpson's Rule, function values are assigned alternating coefficients of 4 and 2, with the first and last values not being multiplied by any coefficient.
• 📈 The function used in the first example is f(x) = x^3, and various f(x) values are calculated for the points based on this function.
• 🧮 The definite integral of f(x) = x^3 from 2 to 10 is accurately calculated using the antiderivative, yielding a result of 2496.
• 🚗 A real-world application of Simpson's Rule involves estimating the displacement of a car based on its instantaneous velocity at specified time intervals.
• ⏱️ In the velocity example, the data points are taken every 5 minutes for the first 30 minutes, requiring conversion of minutes to seconds for accurate calculations.
• 🔍 The average speed of the car over 30 minutes is calculated using total distance divided by total time, resulting in an average speed of approximately 28.1 m/s.
• ⚖️ Simpson's Rule serves as a valuable approximation method for definite integrals, especially useful when working with discrete data points in fields like physics and engineering.

Q & A

What is Simpson's Rule used for?

Simpson's Rule is used to estimate the value of a definite integral, providing a numerical approximation of the area under a curve.

How is the formula for Simpson's Rule structured?

The formula for Simpson's Rule involves the width of rectangles divided by 3, multiplied by a weighted sum of function values at specified points, alternating coefficients of 4 and 2 for the intermediate points.

How do you calculate delta x in the context of Simpson's Rule?

Delta x is calculated as (b - a) / n, where 'a' is the lower limit, 'b' is the upper limit, and 'n' is the number of intervals.

What are the values of 'a', 'b', and 'n' in the example given?

In the example, 'a' is 2, 'b' is 10, and 'n' is 4.

What is the significance of the first and last function values in Simpson's Rule?

The first and last function values are not multiplied by any coefficients in Simpson's Rule, while the intermediate values are multiplied by either 2 or 4.

How does Simpson's Rule compare to actual integration?

Simpson's Rule often provides a good approximation of the definite integral, but the actual integration yields the exact value. In the example, both methods resulted in the same value.

How do you determine the displacement of a car using Simpson's Rule?

To determine the displacement, calculate delta x based on the time intervals and apply Simpson's Rule to the velocity function over those intervals.

What conversion is necessary when calculating displacement from velocity measured in meters per second over intervals in minutes?

Since velocity is in meters per second and time intervals are in minutes, you need to convert the time from minutes to seconds (1 minute = 60 seconds).

How is average speed calculated in the context of the car's journey?

Average speed is calculated by dividing the total distance traveled (displacement) by the total time taken, which must be in the same units (seconds).

What is the average velocity calculated from the given data table?

The average velocity from the given data table is approximately 27.6 meters per second, which is slightly less than the average speed calculated using Simpson's Rule.