Binary Operations (Closure) : ExamSolutions Maths Revision

Summary

In this video, the concept of a set being closed under a binary operation is explored through definitions and practical examples. The presenter explains that a set is closed under an operation if combining any two of its members results in a member of the same set. Using the set of real numbers and a specific set of numbers (1, 2, 3), viewers learn how to construct tables to determine closure under various operations. The video invites viewers to engage with examples and prepares them for the next topic on commutativity.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

What does it mean for a set to be closed under a binary operation?

A set is said to be closed under a binary operation if the operation on any two members of the set results in a member that is also within the set.

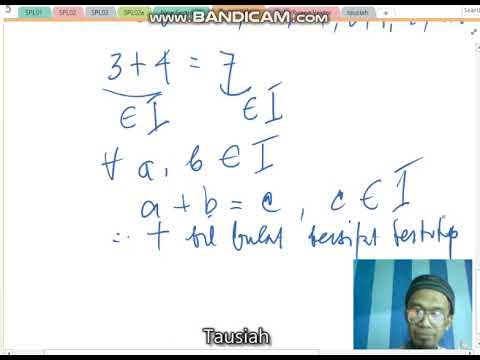
Can you provide an example of a closed set under addition?

Yes, the set of real numbers is closed under addition. For instance, adding two real numbers like 2 and 3 gives 5, which is also a real number.

What happens when we test the set {1, 2, 3} under the operation defined as a star b = a - b?

When testing the set {1, 2, 3} under this operation, we find that not all results are members of the set, such as 1 star 2 = -1, which is not in the set.

How can we check if a set is closed under a binary operation?

We can create a table showing the results of the operation for all combinations of members in the set and check if all results are members of the set.

What did the example with the numbers 0, 2, and 4 illustrate?

The example with the numbers 0, 2, and 4 was used to determine whether the set is closed under a different operation defined as a star operation involving addition and multiplication.

Why is the value 0 important when checking closure in the set {1, 2, 3}?

The value 0 is significant because when calculating certain combinations in the operation a star b = a - b, the result can fall outside the original set, indicating that the set is not closed.

What does it indicate if some results are not contained in the original set during closure testing?

If some results from the operation are not in the original set, it indicates that the set is not closed under that particular binary operation.

What is the next topic mentioned in the video after discussing closure?

The next topic mentioned is the property of commutativity, which is another important aspect of binary operations.

How can students practice determining if a set is closed under a binary operation?

Students can practice by creating their own tables and testing various operations on different sets to see if they are closed.

What was the purpose of constructing a table during the explanation?

The purpose of constructing a table was to systematically examine the results of applying the binary operation to all possible pairs of elements in the set, making it easier to determine closure.