Electrical Engineering: Basic Laws (10 of 31) Kirchhoff's Laws: A Medium Example 1
Summary
TLDRThis video delves into an example of Kirchhoff's laws applied to a single-loop circuit. The instructor walks through solving for current and voltage across components, including resistors and voltage sources. The problem involves summing the voltages around the loop, accounting for drops and rises using assumed current directions. As the analysis unfolds, the calculations reveal a negative current, indicating that the actual current flows in the opposite direction of the initial assumption. By solving the equations, the voltage across one of the sources is found to be -48V and the actual current is 8 amps.
Takeaways
- 🔄 The example in the video focuses on using Kirchhoff's laws in a single-loop circuit with added complexity.
- 🔋 The circuit contains three voltage sources and two resistors, and Kirchhoff’s law states that the sum of voltages in the loop should add up to zero.
- 🔧 Even though the current is assumed to flow clockwise, it may actually flow in the opposite direction, which would affect the voltage drop across resistors.
- ⚡ A key equation used is V = IR to determine the relationship between current and voltage across the resistors.
- 🌀 The voltage drop across the 6-ohm resistor is calculated, taking into account that the assumed current direction may be incorrect.
- 🧮 Substituting values, the final equation is solved to find the current in the circuit.
- 📉 The current is calculated to be -8 amps, indicating that the actual current direction is counterclockwise instead of the assumed clockwise direction.
- 🔋 The voltage across the unknown voltage source is calculated as 48 volts using the current and resistance values.
- 🔄 The result is that the actual current in the circuit flows in the opposite direction to what was initially assumed.
- 📐 The key takeaway is the application of Kirchhoff's laws and Ohm's law to solve for unknown currents and voltages in a more challenging single-loop circuit.
Q & A
What is Kirchhoff's Voltage Law (KVL) and how is it applied in this circuit?
-Kirchhoff's Voltage Law states that the sum of all voltages around any closed loop in a circuit must equal zero. In this example, the sum of the voltage rises and drops as you travel around the loop is calculated to ensure they total zero, helping solve for unknown values like current and voltage.
Why does the direction of the current not matter initially in this analysis?
-The direction of the current doesn't matter because you can assume any direction for analysis. If the current ends up being negative, it means the actual direction is opposite to the assumed one. The sign of the current reveals the true direction after solving the equations.
What is the significance of voltage sources in this circuit?
-There are three voltage sources in the circuit. One of them is unknown, but its voltage is defined in relation to the voltage drop across a resistor. These sources influence the total voltage sum as you traverse the loop.
How is the voltage drop across a resistor calculated?
-The voltage drop across a resistor is calculated using Ohm's law, which states that the voltage drop equals the resistance multiplied by the current (V = IR). If you cross a resistor in the direction of the current, it results in a voltage drop, hence a negative term in the KVL equation.
How does the script handle the relationship between the unknown voltage and the resistor?
-The script states that the voltage across the unknown source is equal to twice the voltage drop across a 6-ohm resistor. This is incorporated into the equations to help solve for both the current and the unknown voltage.
Why do they initially assume the current is clockwise, and what happens when this assumption is incorrect?
-The current is initially assumed to be clockwise for simplicity. If the calculation shows a negative current value, it indicates that the actual current flows in the opposite direction.
How is Ohm's law used to relate the current and the unknown voltage?
-Ohm's law (I = V/R) is applied to the voltage drop across the 6-ohm resistor. By substituting this into the overall KVL equation, the script solves for both the current and the voltage.
What final equation is used to solve for the current in the circuit?
-The final equation used to solve for the current is 12 - 4I + 12I + 4 - 6I = 0, which simplifies to 2I = -16, leading to I = -8 amps.
Why is the current value negative, and what does it indicate about the direction of current flow?
-The current value is negative because the initial assumption about the current direction was incorrect. This means the actual current flows counterclockwise, not clockwise as initially assumed.
What is the voltage across the unknown voltage source, and how is it calculated?
-The voltage across the unknown voltage source is calculated as V = -6 * (-8) = 48 volts. Since the current direction is opposite to the assumed one, the final voltage value is positive.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Electrical Engineering: Basic Laws (11 of 31) Kirchhoff's Laws: A Medium Example 2

KVL and KCL (Circuits for Beginners #11)

Kirchhoff's Law Part 1

Hukum 2 kirchoff rangkaian 2 loop
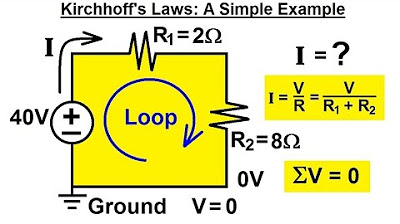
Electrical Engineering: Basic Laws (9 of 31) Kirchhoff's Laws: A Simple Example
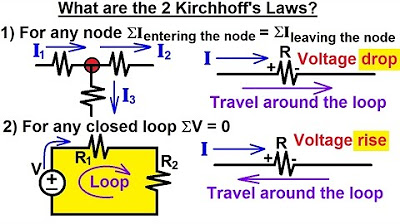
Electrical Engineering: Basic Laws (8 of 31) What Are Kirchhoff's Laws?
5.0 / 5 (0 votes)