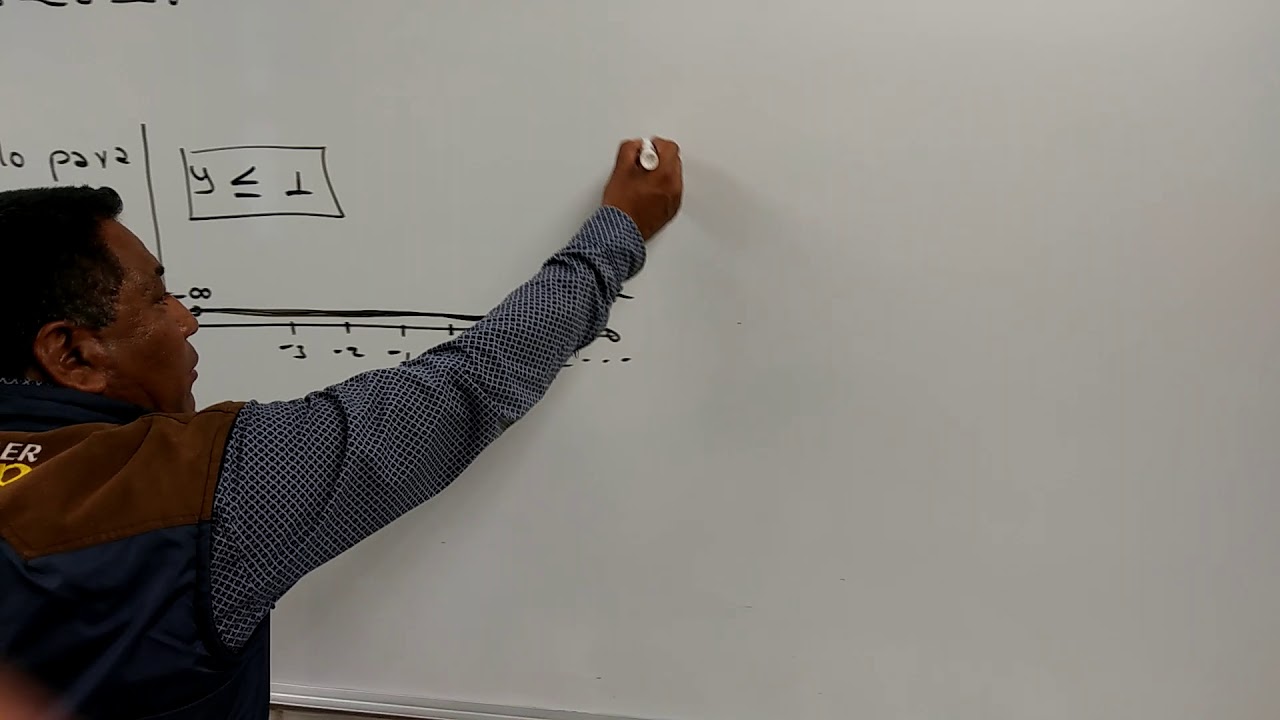Notación de intervalos
Summary
TLDREn esta clase de cálculo, se explica la notación de intervalos utilizando la recta numérica. Se analizan diferentes tipos de intervalos: cerrados, abiertos, y combinaciones de ambos. Ejemplos incluyen intervalos que van de -3 a 5, y otros que se extienden hacia el infinito. Se describe cómo representar estos intervalos gráficamente, con bolitas rellenas para los extremos cerrados y bolitas vacías para los abiertos. Estos conceptos son clave para comprender cómo trabajar con conjuntos de números en cálculo. El profesor invita a los estudiantes a suscribirse y seguir aprendiendo.
Takeaways
- 🔢 Se explica la notación de intervalos utilizando la recta real como base para representar conjuntos de números.
- 📉 Se menciona un intervalo cerrado entre -3 y 5, lo que significa que todos los números entre -3 y 5, incluidos -3 y 5, forman parte del intervalo.
- 🎯 El intervalo cerrado se representa gráficamente con bolitas rellenas para indicar que se incluyen los límites del intervalo.
- 🚪 Un intervalo cerrado en -3 y abierto en 5 implica que incluye -3 pero no 5, lo que se refleja con una bolita rellena en -3 y una bolita sin rellenar en 5.
- 📏 Un intervalo abierto en -3 y abierto en 5 significa que no incluye ni -3 ni 5, representado con bolitas sin rellenar en ambos extremos.
- 📈 Se discute un intervalo cerrado desde -3 hasta infinito, donde el infinito siempre es abierto y se representa extendiendo la recta hacia la derecha.
- ⬅️ También se menciona un intervalo desde menos infinito hasta 5 cerrado, lo que implica que incluye todos los números menores o iguales a 5.
- 🔄 El intervalo abierto desde menos infinito hasta -3 excluye tanto el -3 como los valores hacia el infinito negativo, lo que se refleja en la recta con bolitas sin rellenar.
- 🔍 Las bolitas rellenas o sin rellenar en la recta real ayudan a visualizar si los extremos del intervalo están incluidos o excluidos.
- 📚 Se enfatiza la importancia de la notación de intervalos para su uso en cálculos y matemáticas, siendo una herramienta fundamental en el curso.
Q & A
¿Qué representa una recta real en matemáticas?
-La recta real simboliza todo el conjunto de los números reales, abarcando desde el infinito negativo hasta el infinito positivo.
¿Qué significa que un intervalo esté cerrado en un número?
-Un intervalo cerrado en un número significa que dicho número está incluido dentro del intervalo. Se representa con un corchete como [a].
¿Qué es un intervalo cerrado entre dos números, por ejemplo, entre -3 y 5?
-Un intervalo cerrado entre -3 y 5 significa que el conjunto incluye todos los números reales entre -3 y 5, incluyendo ambos extremos. Se representa como [-3, 5].
¿Cómo se representa un intervalo abierto en uno de sus extremos?
-Un intervalo abierto en uno de sus extremos no incluye ese número. Se usa un paréntesis para representarlo, por ejemplo, (-3, 5] si está abierto en -3 pero cerrado en 5.
¿Cómo se representa un intervalo abierto en ambos extremos?
-Un intervalo abierto en ambos extremos no incluye ninguno de los dos extremos. Se representa con paréntesis en ambos lados, por ejemplo, (-3, 5).
¿Qué sucede cuando un intervalo se extiende hasta el infinito?
-Cuando un intervalo se extiende hasta el infinito, este es siempre abierto, ya que el infinito no es un número finito. Se representa como (a, ∞) o (-∞, b), dependiendo del extremo que se considere.
¿Cómo se representa gráficamente un intervalo cerrado en -3 y abierto en 5?
-Gráficamente, el intervalo cerrado en -3 y abierto en 5 se representa con una bolita rellena en -3 y una bolita sin rellenar en 5, indicando que incluye -3 pero no incluye 5.
¿Qué implica un intervalo que va de menos infinito hasta un número cerrado?
-Un intervalo de menos infinito hasta un número cerrado incluye todos los números menores o iguales a ese número. Se representa como (-∞, b], donde b está incluido en el intervalo.
¿Qué significa un intervalo abierto en un número negativo?
-Un intervalo abierto en un número negativo significa que ese número no está incluido en el intervalo. Por ejemplo, en (-∞, -3), el -3 no está incluido.
¿Qué importancia tiene la notación de intervalos en el cálculo?
-La notación de intervalos es fundamental en el cálculo, ya que permite expresar conjuntos de números, definir dominios de funciones, y analizar límites y continuidad de manera clara y precisa.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)