How to think like a genius ( from a 5x IMO medalist)
Summary
TLDRIn this transcript, a top math Olympiad medalist from Malaysia discusses his experience solving complex problems at the International Mathematical Olympiad (IMO). He explains the importance of identifying patterns and universal ideas within math problems, using intuitive triggers like powers of two or modular arithmetic. However, not all problems fit predictable patterns. He highlights his experience with IMO problem P5, which stumped even experienced teams due to its low-probability solution path. Through trial and error, he ultimately solved it, emphasizing the value of exploring unconventional approaches in problem-solving.
Takeaways
- 🤔 The toughest problem faced at the IMO was P5, a challenging problem during the five years of participation.
- 🏅 The speaker won five medals at the IMO, two of which were gold, making them the most successful competitor in Malaysia's history.
- 🧠 Success in mathematics requires deep analysis of the problem, not just memorizing solutions from past problems.
- 🔍 The goal is to recognize universal ideas and patterns within problems, which can be applied to new and unique challenges.
- 📊 The speaker highlights a common pattern involving powers of two, where induction is often the right approach.
- 🛠 Problem-solving triggers and cues, such as recognizing when to apply modular arithmetic or the pigeonhole principle, are essential for success.
- 🗺 Building a 'mental map' of problem-solving strategies helps in recognizing patterns more effectively over time.
- ⚡ Some problems are designed to go against typical solutions, and students with highly refined problem-solving maps may miss the less obvious solutions.
- ⏳ P5 was one of the toughest problems in terms of time, taking the speaker three and a half hours to solve, highlighting the difficulty of breaking from traditional patterns.
- 🎯 The speaker attributes some success in solving difficult problems to luck, especially when recognizing that conventional approaches were not working.
Q & A
What is the speaker's most challenging problem at the International Mathematical Olympiad (IMO)?
-The speaker's toughest problem at the IMO was Problem 5 (P5), which took him the longest time to solve during his five years of participating.
How many medals did the speaker win at the IMO, and what makes him notable in his country?
-The speaker won five medals at the IMO, including two gold medals, making him the best in the history of Malaysia.
What approach does the speaker suggest for solving mathematical problems?
-The speaker suggests analyzing problems deeply and looking for universal ideas or patterns rather than memorizing specific solutions, as every problem is unique.
What kind of patterns does the speaker believe are important to recognize in math problems?
-The speaker highlights the importance of recognizing patterns, such as problems involving powers of two, which often suggest the use of mathematical induction.
What does the speaker say about the role of 'triggers' in solving math problems?
-The speaker agrees that recognizing 'triggers' in problems can help link the problem to certain solving techniques, making it easier to approach new problems with a mental map of cues.
Can you provide an example of a trigger and its corresponding solving technique, as mentioned by the speaker?
-The speaker gives an example where the equation x² + y² = 3 suggests using modular arithmetic, such as mod 4 or mod 8, to solve it.
Why did some highly experienced students struggle with solving IMO P5, according to the speaker?
-Some experienced students, like the Chinese IMO team, struggled with P5 because their refined mental maps didn't consider the less probable path that the solution required.
How did less experienced students sometimes succeed in solving difficult problems like IMO P5?
-Less experienced students sometimes succeeded because their mental maps were not as refined, allowing them to consider less probable solutions that more experienced students overlooked.
What did the speaker learn from his experience with IMO P5?
-The speaker learned that relying on the most probable path may not always work, and sometimes it's necessary to explore less likely approaches, even if it seems counterintuitive.
How did the speaker finally solve IMO P5, and what role did luck play in it?
-The speaker solved IMO P5 after spending three and a half hours on it. He initially went down the most probable path but later tried a different approach when time was running out. He admits that luck played a role in finding the correct solution in the last 30 minutes.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Talkshow: Indonesian Math Prodigy Goes International
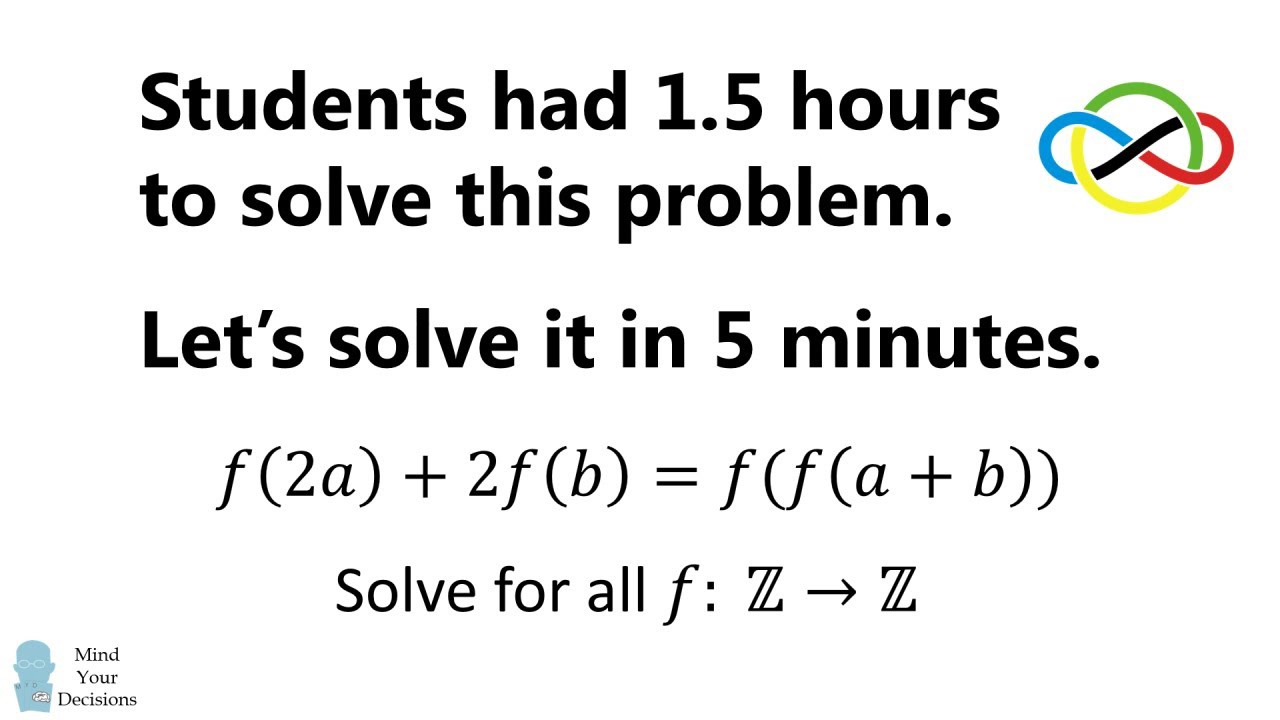
Solving An Insanely Hard Problem For High School Students

Google's new AI crushes everything. True intelligence is here!

Secrets from International Math Olympiad Winner (Exclusive Interview)

MATERI MATEMATIKA YANG WAJIB DIKUASAI UNTUK MENGERJAKAN SOAL-SOAL OSN FISIKA SMA

Hebat! Siswa SMA Indonesia Juarai Olimpiade di Thailand - [Newsline]
5.0 / 5 (0 votes)