Adição e Subtração de Arcos | Trigonometria
Summary
TLDRIn this engaging trigonometry lesson, Sandro Curió explains the addition of angles for sine, cosine, and tangent functions, using mnemonic devices and catchy musical cues to help students remember key formulas. He demonstrates step-by-step how to calculate trigonometric values for angles like 65°, 15°, and 75° by breaking them down into familiar angles. Sandro emphasizes the importance of maintaining or switching signs depending on the operation and provides rationalization techniques for handling tricky denominators. The lesson is lively and designed to help students succeed in their math exams through practical examples and memorable tips.
Takeaways
- 📚 The lesson focuses on the addition of angles in trigonometry, specifically covering sine, cosine, and tangent.
- 🎶 A mnemonic device 'Minha terra tem palmeiras onde canta o sabiá' is used to help remember the sine addition formula.
- ➕ For the sine of two angles (a + b), the formula is: sin(a + b) = sin(a) * cos(b) + cos(a) * sin(b). The sign is kept based on the operation (positive or negative).
- 📐 Example: To find sin(65°), use the addition of known angles 60° and 45° and apply the sine formula.
- 📏 The lesson provides a detailed example of calculating sin(65°) using known values like sin(60°) = √3/2 and cos(45°) = √2/2.
- 🤓 For the cosine of two angles (a + b), a different mnemonic 'Coça coça senta senta' is introduced to help remember the formula.
- ➖ The cosine formula is cos(a + b) = cos(a) * cos(b) - sin(a) * sin(b), and the sign is inverted when using the cosine formula.
- 🔢 Example: To calculate cos(75°), use cos(30° + 45°) and apply the cosine addition formula.
- 🧮 The video also covers the tangent of two angles (a + b) with the mnemonic 'Tem gente que ama, tem gente que beija' to aid in recalling the formula.
- ✔️ The tangent formula for addition is tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a) * tan(b)), with signs kept in the numerator but inverted in the denominator.
Q & A
What is the main topic of the script?
-The main topic of the script is the addition of arcs in trigonometry, focusing on how to calculate sine, cosine, and tangent for angles that are sums or differences of known angles.
How does the script suggest to calculate the sine of 65 degrees?
-To calculate the sine of 65 degrees, the script suggests using the sum of two known angles, 60 degrees and 45 degrees, and then applying the sine addition formula: sin(a + b) = sin(a)cos(b) + cos(a)sin(b).
What is the 'musiquinha' method mentioned in the script?
-The 'musiquinha' method is a mnemonic tool used by the speaker to help remember the trigonometric addition formulas. For example, 'Minha terra tem palmeiras onde canta o sabiá' helps recall the sine addition formula structure.
What is the formula for the sine of a sum of two angles?
-The formula for the sine of a sum of two angles is sin(a + b) = sin(a)cos(b) + cos(a)sin(b).
What is the formula for the cosine of a sum of two angles?
-The formula for the cosine of a sum of two angles is cos(a + b) = cos(a)cos(b) - sin(a)sin(b).
How does the script describe the cosine addition method using a mnemonic?
-For cosine addition, the script uses the mnemonic 'coça coça senta senta' to remember the structure of the formula, while also reminding the user that the sign changes between sine and cosine addition formulas.
How is the tangent of a sum of two angles calculated according to the script?
-The tangent of a sum of two angles is calculated using the formula: tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b)). The mnemonic 'tem gente que ama, tem gente que beija' helps to recall the structure of this formula.
What is the process for rationalizing the denominator in tangent calculations?
-In tangent calculations, if the denominator contains a square root, you multiply both the numerator and denominator by the conjugate of the denominator to eliminate the square root and simplify the expression.
How is the sign handled in trigonometric addition formulas?
-For sine, the sign in the formula remains the same as the original angle addition. For cosine, the sign is inverted: if it's a sum, it becomes a subtraction in the formula, and vice versa.
What is the final answer for sin(65°) according to the script's example?
-The final answer for sin(65°) in the script's example is (√6 + √2) / 4.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Identidades trigonométricas, Identidades de simetría e identidades de suma y resta.
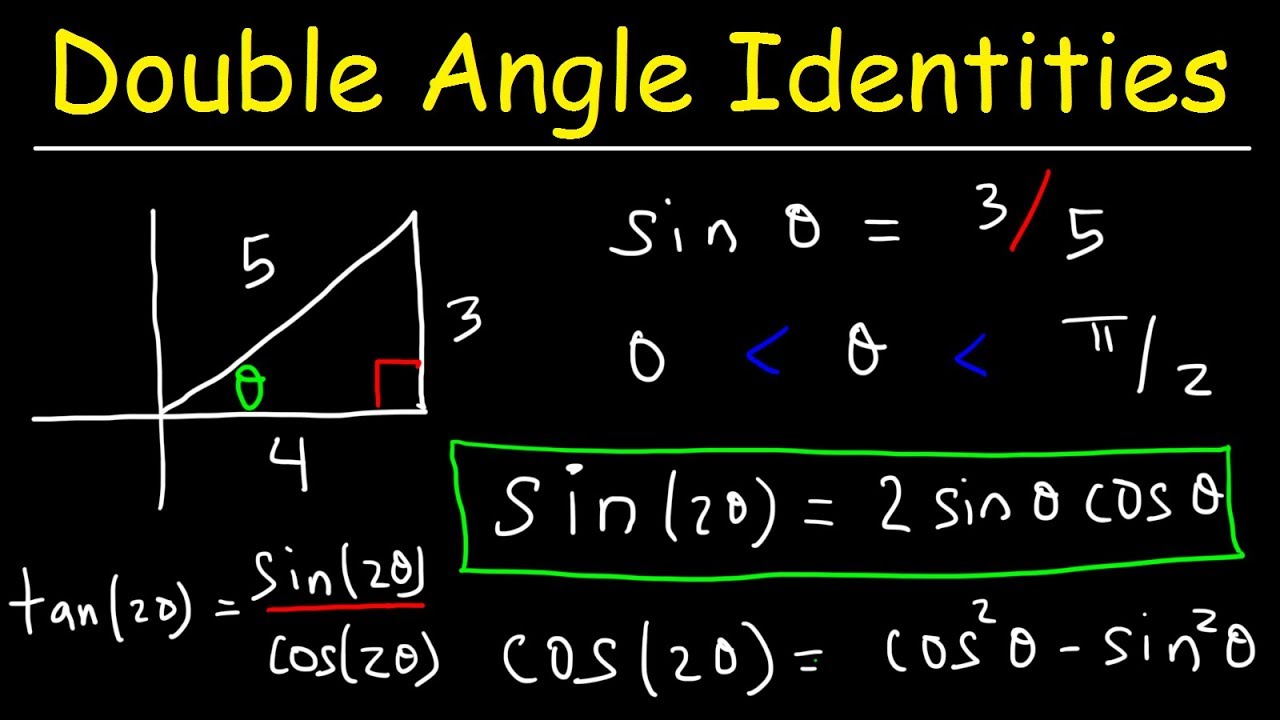
Double Angle Identities & Formulas of Sin, Cos & Tan - Trigonometry

When Do I use Sin, Cos or Tan?

Media Pembelajaran Trigonometri || Jari Trigonometri (Jargonometri)
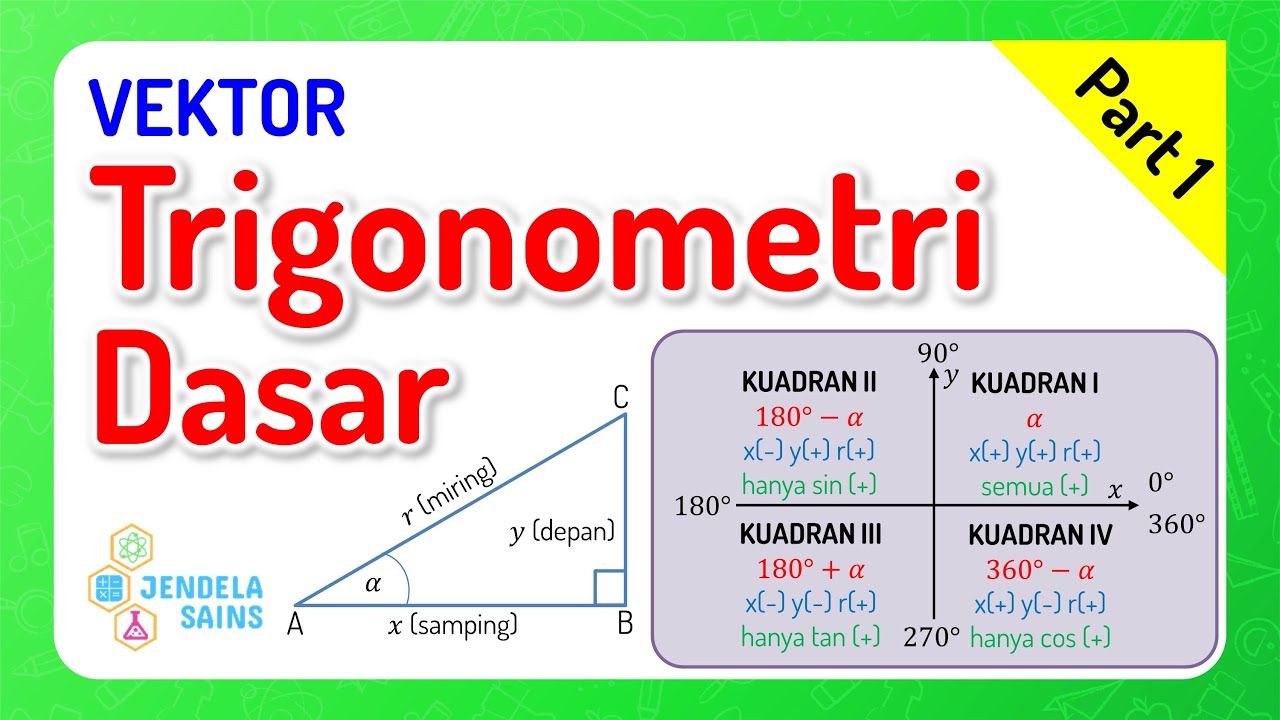
Vektor Fisika • Part 1: Pengantar Trigonometri Dasar
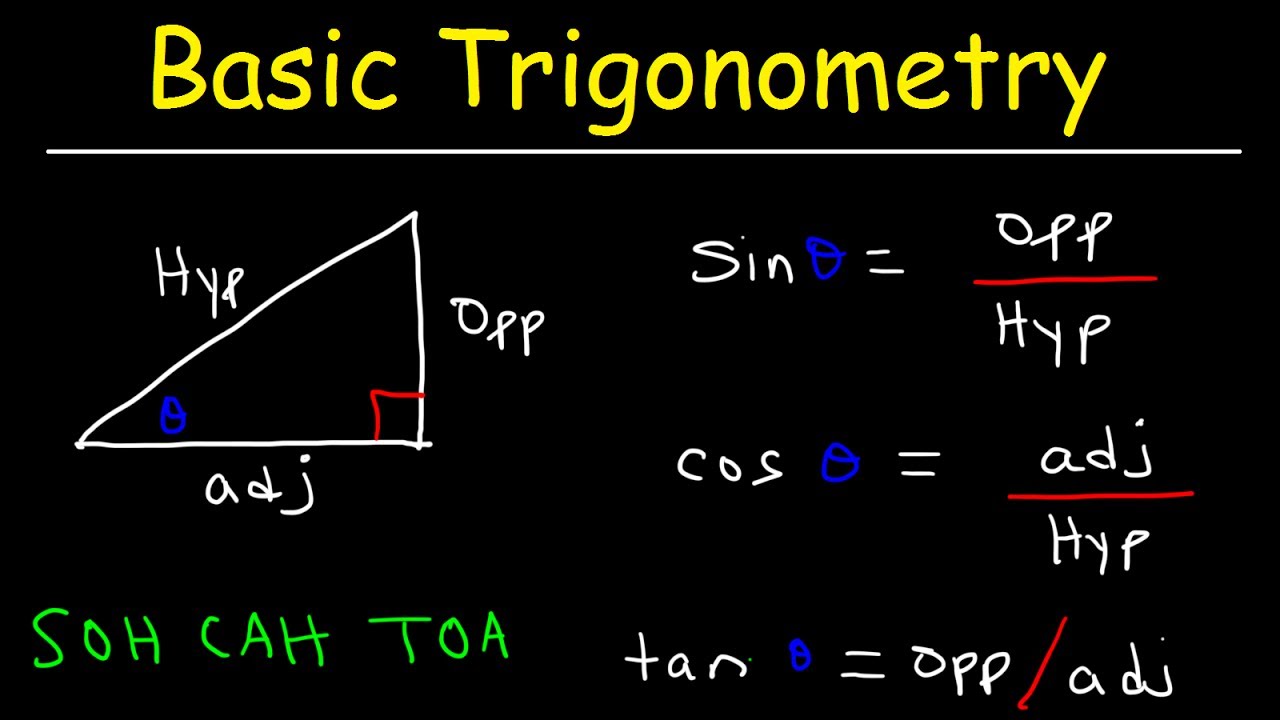
Trigonometry For Beginners!
5.0 / 5 (0 votes)