[Tagalog] Write Polynomial Function into Standard Form, Determine the Degree, Leading Term, Constant
Summary
TLDRIn this educational video, the host explains how to rewrite polynomial functions into standard form and identify key components such as the degree, leading term, leading coefficient, and constant term. Using several examples, the video breaks down the steps involved, including rearranging terms, applying distributive property, and using the FOIL method. The instructor emphasizes understanding the numerical coefficient, exponent rules, and handling positive and negative constants. Viewers are encouraged to engage by liking, subscribing, and asking questions in the comments for further clarification.
Takeaways
- 📘 The video tutorial focuses on explaining polynomial functions.
- 🔑 The presenter teaches how to rewrite polynomial functions into standard form.
- 🔢 The process involves identifying the degree, leading term, leading coefficient, and constant term from the standard form.
- 📐 Example 1 demonstrates converting a simple polynomial without parentheses into standard form: x^2 - 2x + 3.
- 🔑 For Example 1, the degree is 2, the leading term is x^2, the leading coefficient is 1, and the constant term is +3.
- 📝 Example 2 shows how to handle a polynomial with a negative leading term: -5x^3 + 4x - 6.
- 🔑 In Example 2, the degree is 3, the leading term is -5x^3, the leading coefficient is -5, and the constant term is -6.
- 📚 The third example involves polynomial multiplication inside parentheses: x(x^2 - 7) results in x^3 - 7x.
- 🔑 For Example 3, the degree is 3, the leading term is x^3, the leading coefficient is 1, and there is no constant term (it's 0).
- 📖 The fourth example covers the expansion of a polynomial expression: x(x + 2) - 3 simplifies to x^3 - x - 6x.
- 🔑 In Example 4, the degree is 3, the leading term is x^3, the leading coefficient is 1, and the constant term is 0.
- 📢 The presenter encourages viewers to like, subscribe, and turn on notifications for more tutorials.
Q & A
What is a polynomial function?
-A polynomial function is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation.
How do you rewrite a polynomial into standard form?
-To rewrite a polynomial into standard form, you arrange the terms in descending order of their exponents, ensuring each term is in the form of 'coefficient * variable^exponent'.
What is the degree of a polynomial?
-The degree of a polynomial is the highest exponent of the variable present in the polynomial.
How do you find the leading term of a polynomial?
-The leading term of a polynomial is the term with the highest exponent, which is also the term that determines the polynomial's degree.
What is the leading coefficient in a polynomial?
-The leading coefficient is the numerical factor of the leading term, which is the term with the highest exponent in the polynomial.
What is the constant term in a polynomial?
-The constant term in a polynomial is the term that does not contain any variables, it is usually the term with an exponent of zero.
In the given example, what is the standard form of the polynomial 3 - 2x + x^2?
-The standard form of the polynomial 3 - 2x + x^2 is x^2 - 2x + 3.
What is the degree, leading term, leading coefficient, and constant term of the polynomial 4x - 5x^3 - 6?
-The degree of the polynomial 4x - 5x^3 - 6 is 3, the leading term is -5x^3, the leading coefficient is -5, and the constant term is -6.
How do you handle parentheses when rewriting a polynomial into standard form?
-When handling parentheses, you apply the distributive property to multiply the terms inside the parentheses by the term outside, then simplify to obtain the standard form.
In the script, what is the standard form of the polynomial x(x^2 - 7)?
-The standard form of the polynomial x(x^2 - 7) is x^3 - 7x after applying the distributive property.
What method was used to multiply the terms in the polynomial x(x + 2)(x - 3)?
-The FOIL method was used to multiply the terms in the polynomial x(x + 2)(x - 3), resulting in the standard form x^3 - x^2 - 6x.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
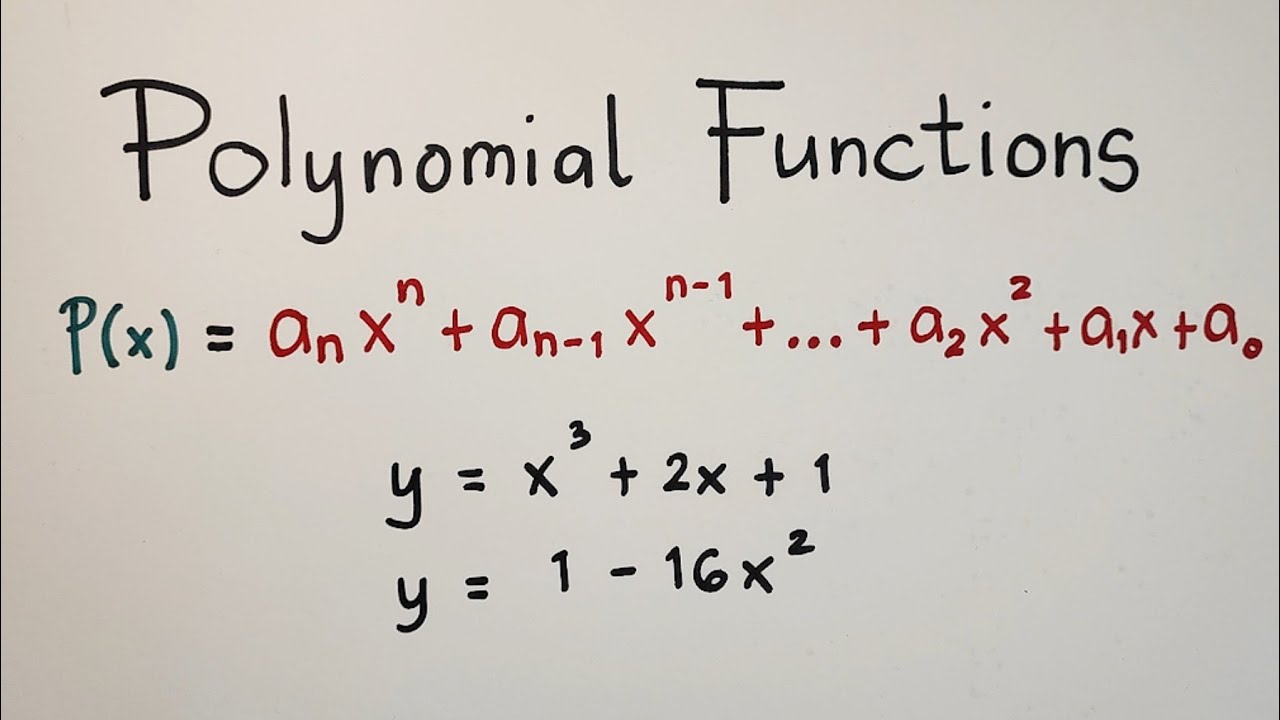
Polynomial Functions - Polynomial Function or NOT? Grade 10 Math Second Quarter

ILLUSTRATING POLYNOMIAL FUNCTIONS || GRADE 10 MATHEMATICS Q2

Illustrate Polynomial Functions | Second Quarter | Grade 10 MELC

AP Precalculus – 1.6 End Behavior and Polynomial Functions

FUNÇÃO AFIM | FUNÇÃO DO 1º GRAU | LEI DE FORMAÇÃO | AULA 1 - Professora Angela Matemática

Grade 10 - Illustrating and graphing polynomial functions | SirABC
5.0 / 5 (0 votes)