Géométrie avec les nombres complexes (1)
Summary
TLDRThis video script discusses a complex problem involving geometric costs, using polar representation to explain concepts. It covers vector differences, complex number arguments, and conditions for specific triangle types (isocceles, rectangle, and equilateral) using complex numbers. The script aims to educate viewers on advanced mathematical concepts through a detailed exploration of these geometric problems.
Takeaways
- 📐 The video discusses a complete solution to a geometric problem involving costs, using polar representation to explain concepts.
- 🔢 It starts with a simple Cartesian coordinate system and moves to polar coordinates, explaining the differences between them.
- 📈 The script explains how to calculate the difference between two points using complex numbers, treating them as vectors.
- 📍 The concept of the argument of a complex number is introduced, which is the angle a segment makes with respect to the real axis.
- 🔄 The video uses the properties of complex numbers to derive conditions for a triangle formed by three complex numbers to be isosceles.
- 📐 It explores the condition for the triangle to be right-angled, involving the arguments of the complex numbers and their norms.
- 🔢 The script delves into the condition for the triangle to be equilateral, using the properties of complex numbers and their norms.
- 📘 The video provides a step-by-step approach to solving the problem, including drawing the triangle and defining a new complex number.
- 🎓 It concludes by emphasizing the importance of understanding the complete solution to practice and reinforce learning.
- 👨🏫 The presenter uses the problem to teach about complex numbers, their arguments, and the geometric interpretation of their properties.
Q & A
What is the main topic of the video?
-The main topic of the video is the resolution of a problem involving costs, which is a geometric problem that explains some interesting things about polar representation.
What is the starting point of the problem discussed in the video?
-The problem starts with a simple Cartesian coordinate system and the difference between two points, which is explained as the difference in imaginary parts.
How does the video explain the concept of vectors in relation to the problem?
-The video explains vectors by showing how the difference between two points can be represented as vectors, and how this works perfectly with the distance between points.
What is the significance of the argument of a complex number in the context of the video?
-The argument of a complex number is significant because it represents the angle that the segment makes with the real axis, which is crucial for understanding the geometric representation of complex numbers.
What is the condition for the triangle formed by complex numbers to be isosceles?
-For the triangle to be isosceles, the condition is that the absolute value of the norms of the complex numbers representing the sides must be equal.
How does the video address the condition for the triangle to be right-angled?
-The video discusses the condition for a triangle to be right-angled by examining the arguments of the complex numbers and stating that the difference between the arguments must be an integer multiple of π/2.
What is the condition for the triangle to be equilateral according to the video?
-For the triangle to be equilateral, the video explains that the complex number representing the triangle must be either equal to e^(iπ/3) or e^(-iπ/3), which corresponds to the angles of an equilateral triangle.
How does the video use the concept of complex numbers to solve the problem?
-The video uses complex numbers to solve the problem by defining a new complex number based on the differences between other complex numbers and then applying geometric properties to find conditions for the triangle formed.
What is the importance of the modulus of complex numbers in the video's explanation?
-The modulus of complex numbers is important because it helps determine the lengths of the sides of the triangle, which is essential for determining the type of triangle (isosceles, right-angled, or equilateral).
How does the video demonstrate the use of polar representation in solving the problem?
-The video demonstrates the use of polar representation by showing how the modulus and argument of complex numbers can be used to determine the properties of the triangle formed by these numbers.
What is the final message or conclusion of the video regarding the problem?
-The final message of the video is that the problem has been completely resolved, and the solution provides a comprehensive understanding of how to work with complex numbers and their geometric interpretations.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Definitions of an Ellipse | MATHS | JEE | Concept of the Day | GB Sir
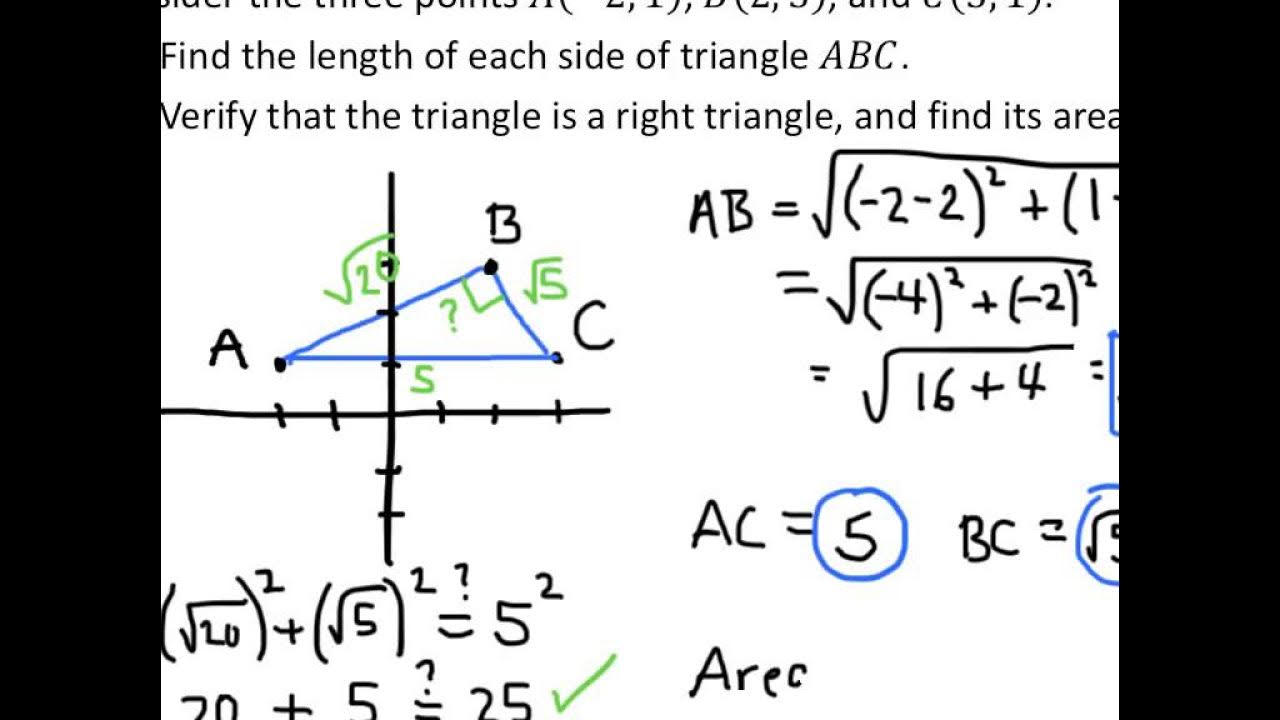
College Algebra Examples: Applications of the Distance and Midpoint Formulas

Pola Bilangan (5) | Barisan dan Deret Geometri

Imaginary Numbers Are Real [Part 7: Complex Multiplication]
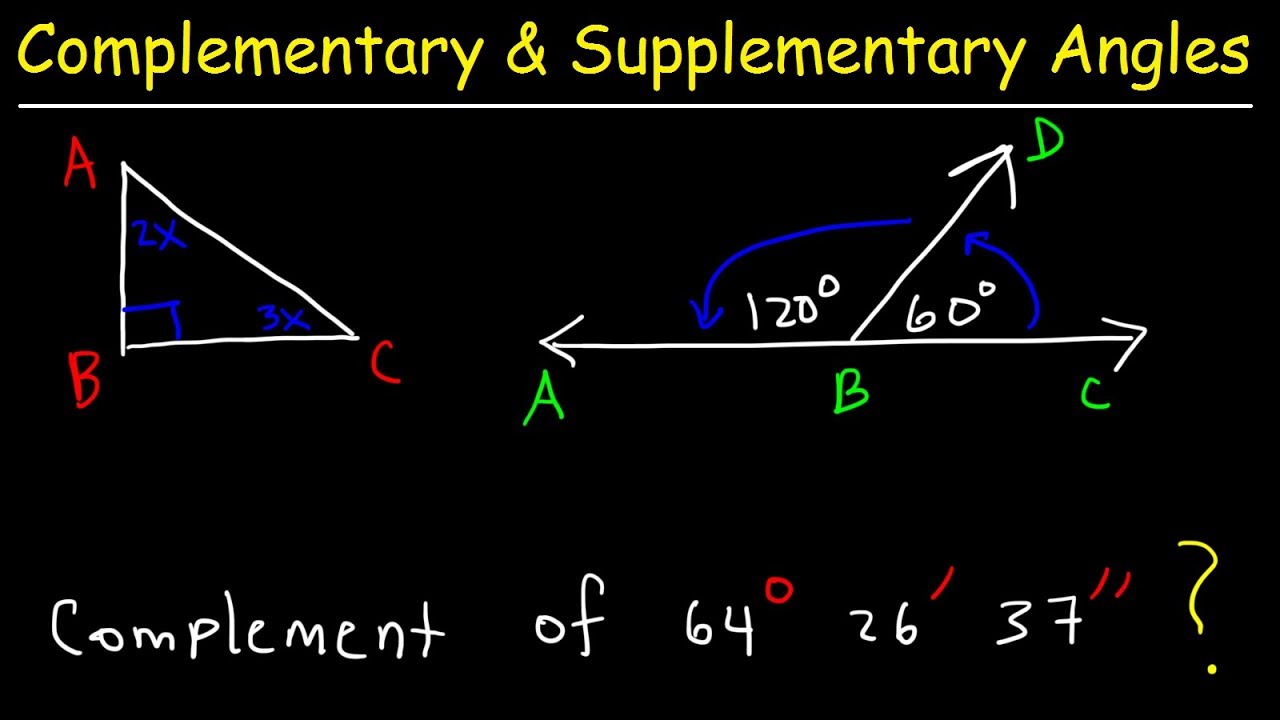
Complementary and Supplementary Angles

Geometric Series | Finding the Sum of Geometric Sequence | Explain in Detailed |
5.0 / 5 (0 votes)