Work/energy problem with friction | Work and energy | Physics | Khan Academy
Summary
TLDRIn this educational video, the host introduces a physics problem involving a biker and rider descending a 500-meter hill with a 5-degree incline, starting from rest. The challenge includes friction, represented by a 60-newton force, which dissipates some energy as heat. The host calculates the biker's final velocity at the hill's base, demonstrating energy conservation principles and the impact of non-conservative forces like friction. The engaging explanation also touches on where the friction might originate and the conversion of mechanical energy to heat.
Takeaways
- 🔄 The law of conservation of energy states that energy cannot be created or destroyed, only transformed.
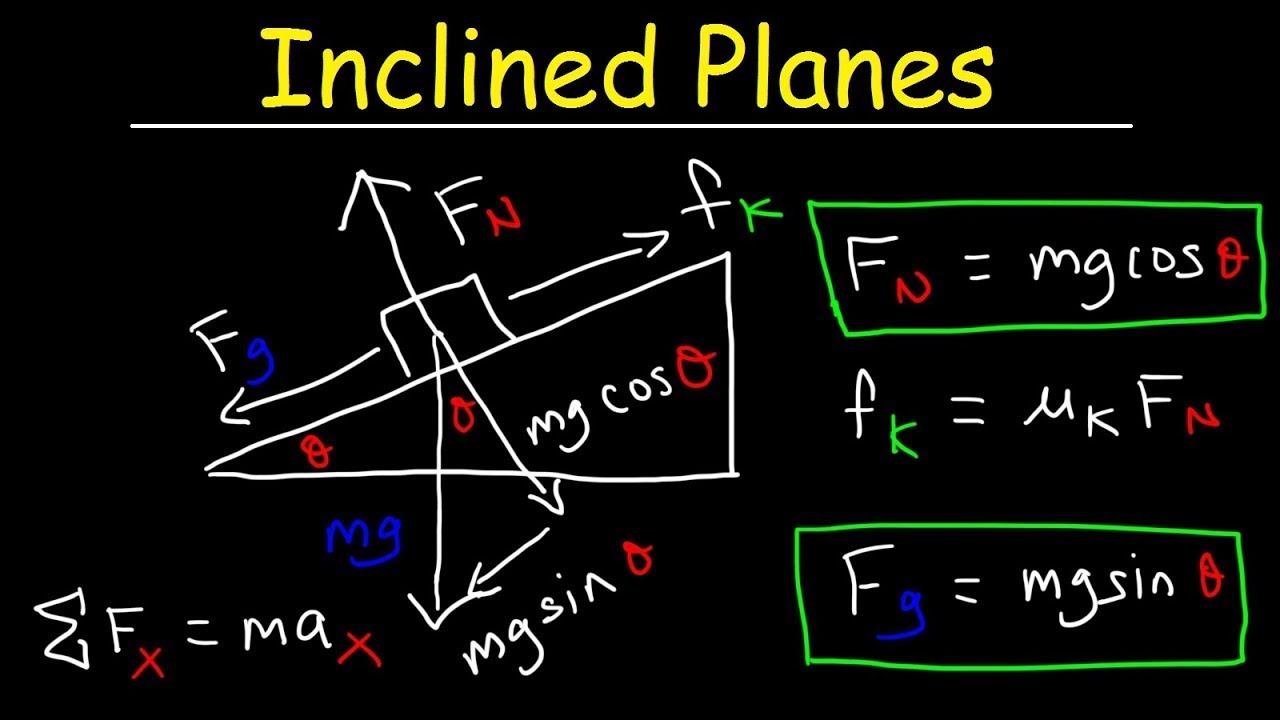
- 🚴♂️ The problem introduces a 90 kg bike and rider starting from rest at the top of a 500-meter long hill with a 5-degree incline.
- 📐 The problem uses trigonometry to calculate the height of the hill, finding it to be 43.6 meters using the sine function.
- 🌐 The potential energy at the start is calculated as mass times gravity times height, resulting in 38,455 joules.
- 🛑 Friction is introduced as a nonconservative force that opposes the motion and consumes mechanical energy.
- 🔢 The average friction force is given as 60 newtons, which is used to calculate the energy lost due to friction.
- 💡 The negative work done by friction is calculated by multiplying the friction force by the distance traveled, resulting in 30,000 joules.
- 🔄 The final energy at the bottom of the hill is the initial potential energy minus the energy lost to friction, equaling 8,455 joules.
- 🚀 The final kinetic energy is calculated using the formula 1/2 mv^2, leading to a final velocity of 13.7 meters per second.
- 🔥 The energy lost to friction is converted into heat, which is a real-world consequence of nonconservative forces.
Q & A
What is the mass of the bike and rider combined?
-The mass of the bike and rider combined is 90 kilograms.
How long is the hill that the bike and rider start from?
-The hill is 500 meters long.
What is the incline of the hill?
-The incline of the hill is 5 degrees.
What is the average friction force acting on the bike and rider?
-The average friction force acting on the bike and rider is 60 newtons.
What is the initial potential energy of the bike and rider at the top of the hill?
-The initial potential energy is calculated as mass times the acceleration of gravity times height, which is 90 kg * 9.8 m/s² * 43.6 m, equaling approximately 38,455 joules.
How is the height of the hill calculated?
-The height of the hill is calculated using the sine function with the given angle and hypotenuse, which is 500 meters * sin(5 degrees), resulting in 43.6 meters.
What happens to the potential energy at the bottom of the hill?
-At the bottom of the hill, the potential energy is mostly converted into kinetic energy, but some is lost to friction.
How is the energy lost to friction calculated?
-The energy lost to friction is calculated as the negative work done by friction, which is the friction force times the distance moved against the force, or -60 N * 500 m, equaling -30,000 joules.
What is the final kinetic energy of the bike and rider at the bottom of the hill?
-The final kinetic energy is the initial potential energy minus the energy lost to friction, which is 38,455 joules - 30,000 joules, equaling 8,455 joules.
What is the final velocity of the bike and rider at the bottom of the hill?
-The final velocity is calculated by taking the square root of the final kinetic energy divided by the mass, which is sqrt(8,455 joules / 45 kg), resulting in approximately 13.7 meters per second.
Where does the energy lost to friction go?
-The energy lost to friction is converted into heat, which could be felt as warmth in the bike's components or due to air resistance.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)