Modelacion Matemática - Introducción al Mundo de la Modelación
Summary
TLDREste vídeo introductorio aborda la modelación matemática, explicando qué es un modelo matemático y cómo se desarrolla. Se enfatiza que el proceso no es lineal y que los modelos mentales son esenciales para interpretar y solucionar problemas. Se discuten ejemplos de modelos como el de Malthus para el crecimiento poblacional y uno de optimización para la venta de frutas. El vídeo también destaca la importancia de la evaluación y la implementación de modelos y cómo estos pueden ayudar a mejorar los modelos mentales y tomar decisiones informadas.
Takeaways
- 🌐 El proceso de modelación matemática no es lineal y puede variar dependiendo de la percepción individual del mundo.
- 🧠 Los modelos mentales juegan un papel crucial en la generación de estrategias para resolver problemas y tomar decisiones.
- 🏗️ La calidad de los modelos mentales depende de la calidad de la información utilizada para construirlos.
- ⚖️ Se hace un esfuerzo consciente para simplificar los modelos matemáticos al excluir variables irrelevantes y reducir la complejidad.
- 🔍 Es fundamental diferenciar entre variables exógenas y endógenas al formular un modelo matemático.
- 📊 Los modelos matemáticos son útiles para representar sistemas, analizar fenómenos y predecir comportamientos bajo diferentes escenarios.
- 📉 Un ejemplo clásico de modelo matemático es la fórmula del área de un triángulo, que se aprende temprano y es ampliamente reconocida.
- 📈 Los modelos lineales, como la recta de mejor ajuste, son una herramienta común para aproximar relaciones entre variables.
- 🌱 El modelo de crecimiento poblacional de Malthus es un ejemplo de modelo que ilustra cómo los modelos pueden predecir comportamientos a lo largo del tiempo.
- 🔎 La evaluación de modelos es crucial para garantizar que sean robustos y aplicables en el mundo real, más allá de condiciones extremas.
Q & A
¿Qué es la modelación matemática?
-La modelación matemática es el proceso de crear un modelo que representa un sistema o problema de una manera que pueda ser analizada matemáticamente.
¿Cuál es la importancia de la modelación matemática en la toma de decisiones?
-La modelación matemática ayuda a tomar decisiones informadas al proporcionar una representación idealizada de objetos, personas, conceptos, etc., lo que permite prever resultados y estrategias antes de implementar acciones en el mundo real.
¿Por qué el proceso de modelación no es lineal?
-El proceso de modelación no es lineal porque implica un ir y venir entre diversas actividades o etapas, y a menudo requiere reiterar pasos o cambiar de enfoque dependiendo de los resultados obtenidos y la información nueva.
¿Qué es un modelo mental y cómo se relaciona con la modelación matemática?
-Un modelo mental es una representación idealizada de una situación en la mente, y es la base desde la cual se desarrollan modelos matemáticos. Estos modelos mentales ayudan a interpretar y entender mejor el mundo real y a generar estrategias para solucionar problemas.
¿Qué es un modelo matemático y cómo difiere de un modelo mental?
-Un modelo matemático es una representación formal y estructurada de un sistema o problema usando notación matemática, mientras que un modelo mental es una representación conceptual y subjetiva en la mente de una persona.
¿Cuál es la función de un modelo matemático en el estudio de ecuaciones diferenciales ordinarias?
-En el estudio de ecuaciones diferenciales ordinarias, un modelo matemático permite describir y predecir la evolución de una cantidad con respecto al tiempo o a otras variables, como se ve en el modelo de crecimiento poblacional de Malthus.
¿Cómo se utiliza la dimensión lineal en la modelación matemática?
-La dimensión lineal se utiliza en la modelación matemática para aproximar la relación entre dos variables usando una recta, lo que permite hacer predicciones basadas en la tendencia lineal observada.
¿Qué es un modelo de optimización y cómo se aplica en contextos prácticos?
-Un modelo de optimización es un tipo de modelo matemático diseñado para encontrar la mejor solución en términos de costos o beneficios bajo ciertas restricciones. Se aplica en contextos prácticos como la toma de decisiones empresariales, la planificación de recursos y la asignación de tareas.
¿Cómo se evalúa la validez de un modelo matemático?
-La validez de un modelo matemático se evalúa verificando si reproduce adecuadamente el comportamiento del problema estudiado, si es robusto bajo condiciones extremas y si las soluciones obtenidas son aplicables y útiles en el mundo real.
¿Cuáles son los métodos para resolver modelos matemáticos?
-Los métodos para resolver modelos matemáticos incluyen el análisis analítico, los métodos numéricos y el enfoque cualitativo, cada uno con aplicaciones específicas dependiendo de la naturaleza y la complejidad del modelo.
¿Cómo se relaciona la implementación de un modelo matemático con la generación de nuevos retos?
-La implementación de un modelo matemático en el mundo real puede revelar nuevas dinámicas o problemas no considerados previamente, lo que genera nuevos retos y puede requerir la actualización o creación de nuevos modelos para abordar estas situaciones.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Qué es un ensayo? Qué es un ensayo literario? - Qué es?

Análisis de Sensibilidad de la Función Objetivo

Problema de APLICACIÓN DE LÍMITES / Ejercicio N° 1 / (Nivel: Medio)

IONES ☣ CATIONES Y ANIONES ☣¿Qué son los iones ☣Explicación fácil y completa

La derivada en una taza de café: una aplicación práctica de la vida cotidiana. #QuédateEnCasa
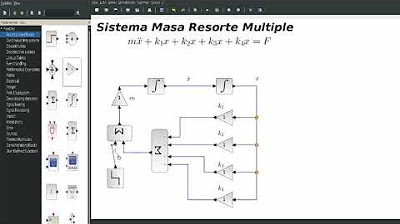
Simulación Sistema Masa Resorte Multiple XCos Part1
5.0 / 5 (0 votes)
