60. Integral de función exponencial, completando la derivada
Summary
TLDREn este vídeo tutorial de 'Mate fácil', se explica cómo realizar la integral de una función exponencial. Se utiliza la fórmula de la integral de exponencial de 'B', donde 'B' es el exponente, en este caso 'x cuadrada'. Se muestra cómo derivar 'x cuadrada' para obtener 'db', que es '2x', y cómo ajustar la integral para no alterar la expresión inicial. Finalmente, se propone a los espectadores intentar realizar una integral similar y se invita a dejar comentarios y suscripciones para más contenido.
Takeaways
- 📘 La integral de una función exponencial se puede calcular usando la fórmula de la integral de la exponencial de 'b' por 'db' igual a la exponencial de 'b'.
- 🔍 Para integrar una función exponencial, es necesario identificar el exponente 'b' y luego derivar la función para obtener 'db'.
- 📐 En el ejemplo dado, el exponente 'b' es 'x cuadrada', y su derivada 'db' es '2x'.
- 🔄 Al derivar, se debe tener cuidado de no alterar la expresión inicial al añadir la derivada '2x' multiplicando y luego dividiendo por 2 para mantener la integral correcta.
- 📝 Se añade un factor de 2 multiplicando y se saca un 2 dividiendo para balancear la integral y aplicar la fórmula de la integral de exponencial.
- 🧮 La integral de la exponencial de 'x cuadrada' por '2x dx' se resuelve sustituyendo 'b' por 'x cuadrada' y añadiendo la constante de integración al final.
- 📖 Se propone un desafío similar para que el espectador pruebe su comprensión: integrar 'x cuadrada por e a la x cuadrada menos 5 dx'.
- 🔄 En la integral propuesta, la 'x cuadrada' se usa para facilitar la derivación del exponente, ya que la derivada de 'x cúbica' es '3x cuadrada'.
- 📝 Al derivar 'x cúbica', se obtiene '3x cuadrada', y se procede a ajustar la integral añadiendo un tercio y utilizando la fórmula de la integral de exponencial.
- 👍 Se alienta a los espectadores a interactuar con el video, dejando 'likes', comentarios y suscripciones para recibir más contenido similar.
Q & A
¿Qué tipo de integral se resuelve en el video?
-Se resuelve una integral de una función exponencial, específicamente de la forma e^(x^2) * x^2.
¿Cuál es la fórmula que se utiliza para integrar funciones exponenciales?
-La fórmula utilizada es la integral de e^(Bx) * dx, que es igual a (1/B) * e^(Bx) + C, donde B es el exponente de la exponencial.
¿Cómo se determina el valor de B en la integral exponencial?
-En este caso, B es igual a x^2, ya que es el exponente de la función exponencial e^(x^2).
¿Qué es db y cómo se relaciona con la integral?
-Db es la derivada de x^2, que es 2x, y se utiliza para completar la derivada en la fórmula de integración de funciones exponenciales.
¿Por qué se agrega un factor de 2 en la integral y luego se divide por 2?
-Se agrega un 2 multiplicando y luego se divide por 2 para compensar el factor que se agrega al derivar x^2, asegurándose de no alterar la expresión inicial de la integral.
¿Cuál es el resultado de la integral e^(x^2) * x^2 dx?
-El resultado es (1/2) * e^(x^2) + C, donde C es la constante de integración.
¿Qué integral se propone como desafío al final del video?
-Se propone la integral de x^3 * e^(x^3 - 5) dx como un desafío similar al que se resolvió en el video.
¿Cómo se puede simplificar la integral x^3 * e^(x^3 - 5) dx?
-Puede simplificarse al notar que x^3 nos ayuda a completar la derivada del exponente, y luego se utiliza la fórmula de la integral exponencial.
¿Cuál es la derivada de x^3 y cómo se relaciona con la integral propuesta?
-La derivada de x^3 es 3x^2. Esto se relaciona con la integral porque al integrar e^(x^3) * x^3 dx, se puede usar la fórmula de la integral de funciones exponenciales después de ajustar el exponente.
¿Cómo se puede integrar la función e^(x^3 - 5) * x^3 dx?
-Después de ajustar el exponente y la derivada, se puede aplicar la fórmula de la integral de funciones exponenciales para resolver la integral.
¿Cómo se puede verificar si la respuesta a la integral propuesta es correcta?
-Se puede verificar en el siguiente video que el canal publique, donde se espera que se revele la solución y se pueda comparar con el resultado obtenido.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

07. Valor de una función con valor absoluto

02. Modelo poblacional, población de bacterias, Ecuaciones Diferenciales

06. Límite con indeterminación 0/0

07. Límite con indeterminación 0/0
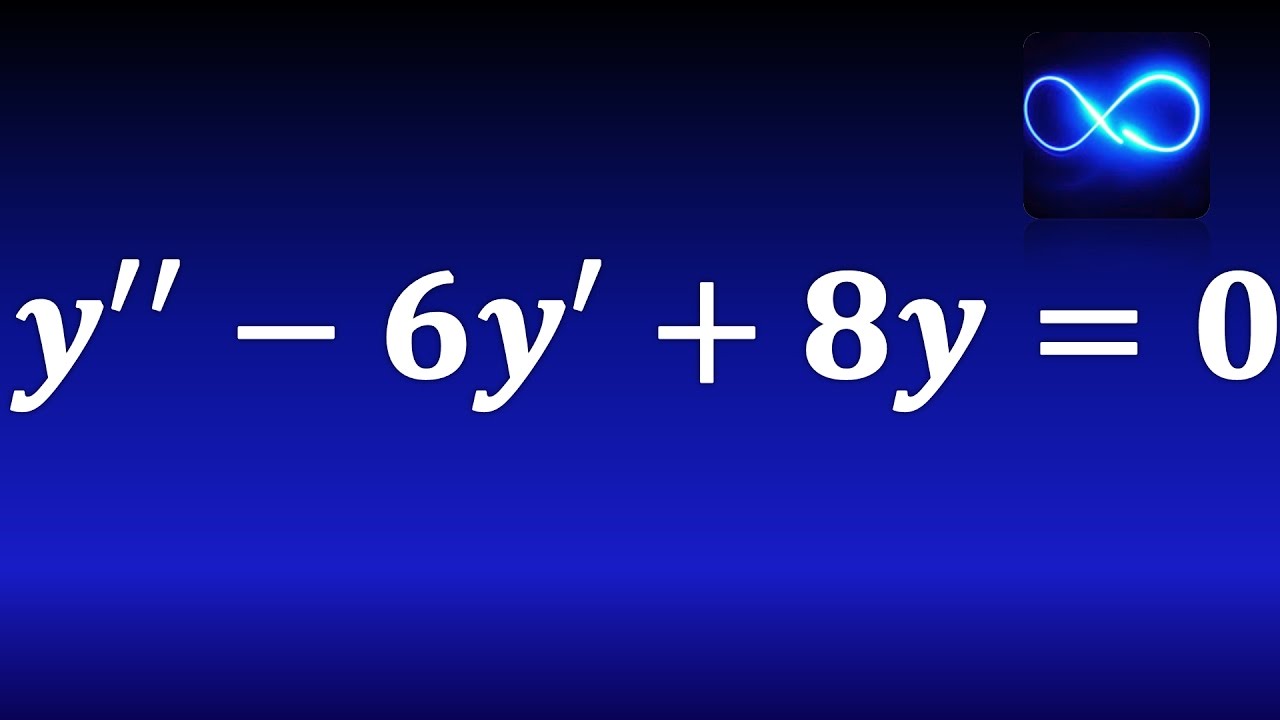
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO

1. Ecuación diferencial de variables separables
5.0 / 5 (0 votes)
