Unidad 1 1.3 Expresiones Algebraicas Suma, Resta, Multiplicación y División
Summary
TLDREn este vídeo tutorial, Galvis L explica conceptos de álgebra, centrándose en la suma, resta, multiplicación y división de expresiones algebraicas. Detalla cómo agrupar términos semejantes y realizar operaciones con variables como x, y y z. Posteriormente, aborda la división sintética, destacando su importancia en cálculo integral. Se ilustra con ejercicios paso a paso, proponiendo tareas similares para práctica adicional.
Takeaways
- 📚 Se está trabajando con el punto 1.3 del primer capítulo de la guía de la UNAM 2020 para áreas 1, 2 y 3.
- 🔢 Se aborda la suma, resta, multiplicación y división de expresiones algebraicas, con énfasis en que la división puede ser complicada.
- 📈 Al sumar y restar, se agrupan términos semejantes, es decir, aquellos que tienen la misma variable.
- 🔄 Se ilustra cómo se manejan las variables 'x', 'y' y 'zeta' en las operaciones algebraicas.
- 📝 Se explica que en la multiplicación de binomios, se multiplica el primer término del binomio por cada término del otro binomio y se sigue con el segundo término.
- 📉 Se resaltan las leyes de signos en la multiplicación: más por menos da menos, más por más da más, menos por menos da más y menos por más da menos.
- 📖 Se enfatiza la importancia de entender la división sintética, que se aplicará más adelante en cálculo integral.
- 📐 Se menciona que el grado de un polinomio es el término con el mayor exponente en su variable.
- 🔑 Se presentan tres casos para la división sintética: cuando el grado del polinomio en el numerador es mayor, menor o igual al del denominador.
- 📘 Se detalla el proceso de división sintética con un ejemplo, destacando la importancia de encontrar el término que haga que el numerador sea divisible por el denominador.
Q & A
¿Qué tema se aborda en el punto 1.3 del primer capítulo de la guía de la UNAM 2020?
-El tema tratado es el manejo de expresiones algebraicas, específicamente la suma, resta, multiplicación y división.
¿Qué variables se mencionan en el video para ejemplificar las expresiones algebraicas?
-Se mencionan las variables x, y y zeta para ejemplificar las expresiones algebraicas.
¿Cómo se definen los términos semejantes en el contexto de las expresiones algebraicas?
-Los términos semejantes son aquellos que pueden ser operados en suma y resta, generalmente son términos que contienen la misma variable elevada al mismo grado.
¿Cuál es la diferencia entre la suma y la resta de expresiones algebraicas según el video?
-La suma y la resta de expresiones algebraicas implican agrupar y operar únicamente términos semejantes, es decir, aquellos que tienen la misma variable y el mismo exponente.
¿Cómo se multiplican dos binomios según el método explicado en el video?
-Para multiplicar dos binomios, se multiplica el primer término del primer binomio por cada término del segundo binomio, y luego se hace lo mismo con el segundo término del primer binomio.
¿Qué significa la ley de signos en el contexto de la multiplicación de expresiones algebraicas?
-La ley de signos indica cómo se manejan los signos durante la multiplicación: si se multiplican dos números o términos con el mismo signo, el resultado es positivo; si son de signos diferentes, el resultado es negativo.
¿Qué complicaciones surgen con la división en el contexto de las expresiones algebraicas?
-La división se vuelve complicada porque puede requerir técnicas como la división sintética, que implica operar con términos y grados de polinomios.
¿Qué es la división sintética y cómo se relaciona con la división de expresiones algebraicas?
-La división sintética es una técnica para dividir expresiones algebraicas, especialmente útil cuando se trabaja con polinomios, y se basa en la eliminación progresiva de términos a medida que se lleva a cabo la división.
¿Cómo se determina si se puede realizar la división sintética entre dos polinomios?
-Se puede realizar la división sintética si el grado del polinomio del numerador es mayor o igual al del denominador.
¿Cuál es el grado de un polinomio y cómo se determina?
-El grado de un polinomio es el exponente más alto de la variable en su término de mayor grado. Se determina observando el término que contiene la variable elevada a la potencia más alta.
¿Cómo se abordan los ejercicios de división sintética en el video?
-Los ejercicios de división sintética se abordan siguiendo un procedimiento paso a paso, donde se elige un término para dividir y se multiplica por cada término del numerador, luego se restan los productos para obtener un nuevo numerador y se repite el proceso hasta obtener el resultado y el residuo.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Pensamiento matemático 3. Progresión 3a. Suma de funciones
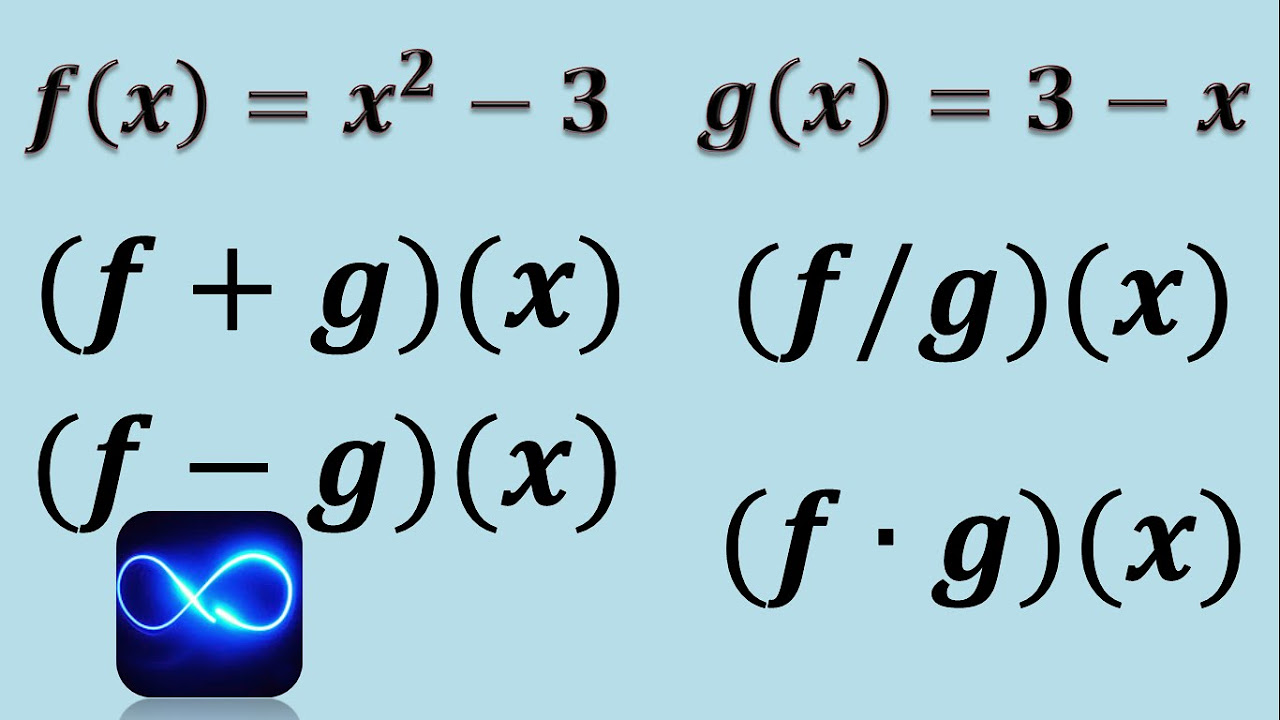
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 2)

Expresiones algebraicas | Curso de Álgebra
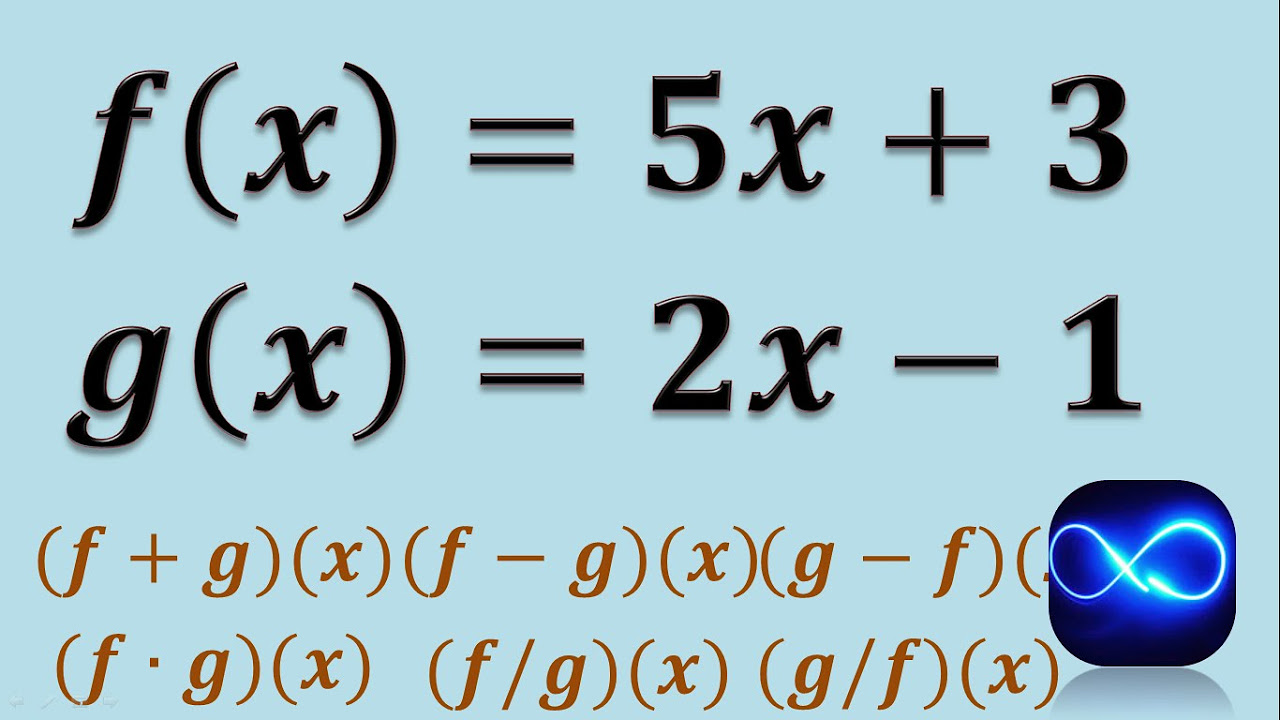
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 1)

OPERACIONES con Funciones 🔢 Suma, Resta, Multiplicación y División

Combinación de funciones. Operación de funciones (suma, resta, multiplicación, división).
5.0 / 5 (0 votes)
