SPM Mathematics Form 4 (Quadratic Functions & Equations in One Variable) Chapter 1 Complete Revision

Summary

Teacher Daisy's video script covers quadratic functions and equations in one variable. It explains the concept, general form, and characteristics of quadratic equations. The script discusses determining quadratic expressions, the graph's shape (a parabola), vertex as the max or min point, and finding these points. It explores the effects of 'a', 'b', and 'c' on the graph's shape and position. The script also teaches finding roots through factorization and graphical methods, and includes examples for clarity.

Takeaways

• 📐 The term 'quadratic' comes from 'quad' meaning square, as the variable is squared in quadratic expressions and equations.
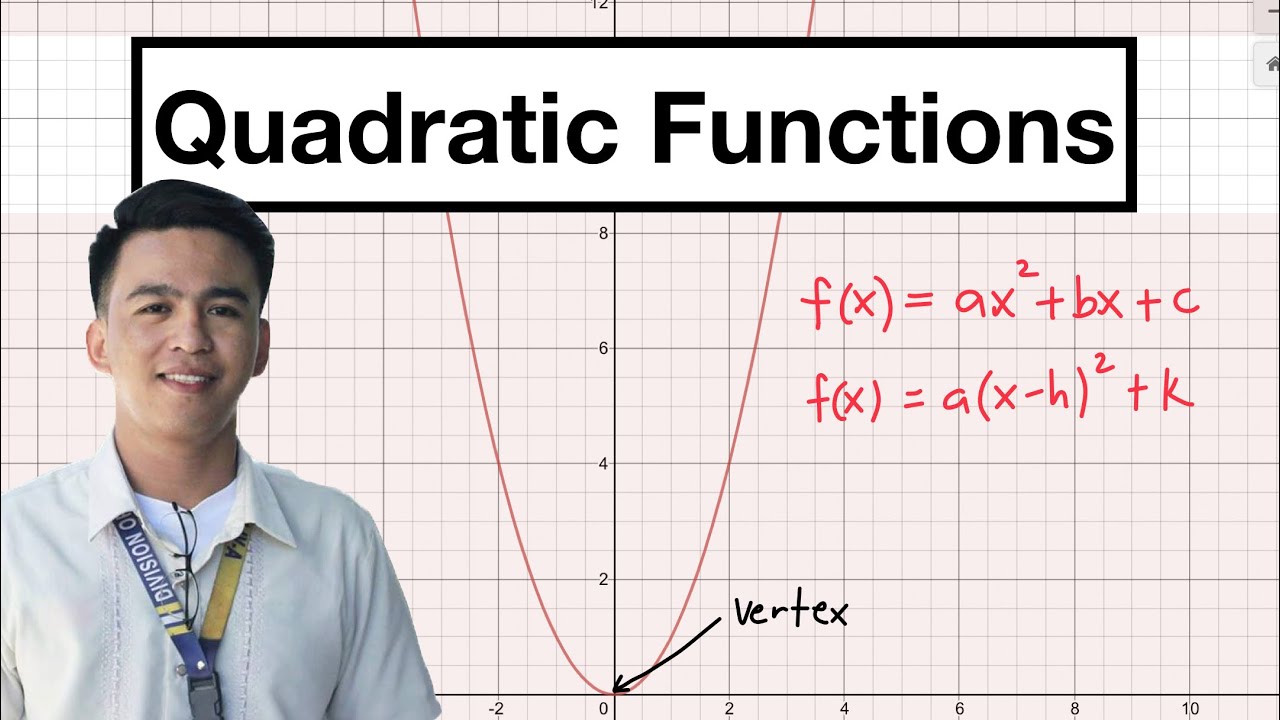
• 🔢 A quadratic equation in one variable is an equation with the highest power of the variable being two, such as ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0.
• 📉 The graph of a quadratic function is a parabola, which is U-shaped and can open upwards or downwards depending on the sign of a.
• 🔍 The vertex of a parabola is the maximum or minimum point and can be found using the formula x = -b/(2a).
• 📈 The value of a affects the width and direction of the parabola's opening: larger |a| results in a narrower parabola, and the sign of a determines if it opens upwards (positive) or downwards (negative).
• 📍 The value of b determines the position of the axis of symmetry relative to the y-axis.
• 📈 The value of c determines the y-intercept of the parabola, which is the point where the graph intersects the y-axis.
• 🔑 Quadratic functions can have real roots, imaginary roots, or touch the x-axis at one point, depending on the discriminant (b^2 - 4ac) of the equation.
• 🔍 To find the roots of a quadratic equation, methods such as factorization, the quadratic formula, completing the square, or graphing can be used.
• 📊 The graphical method to determine roots involves finding the points where the graph intersects the x-axis.
• 🎨 Sketching the graph of a quadratic function requires showing the correct shape, y-intercept, and x-intercepts or points that the graph passes through.

Q & A

What is the definition of a quadratic function?

A quadratic function is a function of the form f(x) = ax^2 + bx + c, where a, b, and c are numbers with a not equal to zero.

What is the general form of a quadratic equation?

The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants and a cannot be zero.

What does the term 'quadratic' mean in the context of mathematics?

The term 'quadratic' comes from 'quad' meaning square because the variable is squared in the equation.

How can you determine if an expression is a quadratic expression in one variable?

An expression is a quadratic expression in one variable if it has only one variable, and the highest power of the variable is two.

What is the relationship between the value of 'a' and the direction in which the graph of a quadratic function opens?

If a is greater than 0, the graph opens upward. If a is less than zero, the graph opens downward.

What is the vertex of a parabola?

The vertex of a parabola is the bottom or top of the 'U' shape, also called the turning point or stationary point.

How do you find the x-value of the vertex of a quadratic function?

To find the x-value of the vertex, you add up the two roots and divide by two.

What is the axis of symmetry of the graph of a quadratic function?

The axis of symmetry is a vertical line drawn through the vertex of the parabola.

How does the value of 'b' affect the position of the axis of symmetry in a quadratic function?

The value of 'b' determines the position of the axis of symmetry. If a is positive and b is positive, the axis of symmetry lies to the left of the y-axis, and so on.

What are the different methods to determine the roots of a quadratic equation?

There are four methods to determine the roots of a quadratic equation: 1) factorization, 2) quadratic formula, 3) completing the square, and 4) graphing.

How can you sketch the graph of a quadratic function?

To sketch the graph of a quadratic function, you should show the correct shape of the graph, the y-intercept, and the x-intercept or points that pass through the graph.

Outlines

00:00

📚 Introduction to Quadratic Functions and Equations

Teacher Daisy introduces the concept of quadratic functions and equations in one variable. The term 'quadratic' is derived from 'quad' meaning square, as the variable is squared. Quadratic expressions are of the form ax^2 + bx + c, and a quadratic equation is an equation with one variable and the highest power of the variable is two, represented as ax^2 + bx + c = 0, where a, b, and c are constants with a ≠ 0. The teacher provides examples to determine whether expressions are quadratic, explaining that the presence of variables with powers other than two or multiple variables disqualifies them as quadratic. The concept of a quadratic function, denoted as fx = ax^2 + bx + c, is also introduced, emphasizing that a ≠ 0. The video explains that quadratic functions have a many-to-one relationship and their graphs resemble a 'U' shape, known as a parabola. The vertex of the parabola, which can be a maximum or minimum point, is determined by the sign of 'a'. The video also covers how to find the vertex and axis of symmetry of a quadratic function.

05:02

📈 Effects of Coefficients on Quadratic Graphs

This section discusses how the values of coefficients 'a', 'b', and 'c' affect the graph of quadratic functions. The value of 'a' determines the direction in which the parabola opens; if 'a' > 0, it opens upwards, and if 'a' < 0, it opens downwards. The magnitude of 'a' affects the width of the parabola. The value of 'b' determines the position of the axis of symmetry, which can be to the left or right of the y-axis depending on the sign of 'b' and 'a'. The value of 'c' determines the y-intercept of the graph. An example is given to find the value of 'c' for a quadratic function passing through a specific point. The roots of a quadratic function, which are the points where the graph intersects the x-axis, are also explained. The video provides examples to determine whether certain values are roots of a given quadratic equation and how to find the roots using different methods such as factorization and graphing.

10:02

🔍 Factorization and Graphical Methods for Finding Roots

The video script explains two methods for finding the roots of a quadratic equation: factorization and graphical methods. In the factorization method, the equation is first expressed in the form ax^2 + bx + c = 0, then factored, and each factor is set to zero to solve for 'x'. Examples are provided to demonstrate how to find the roots using the factorization method, including cases with a greatest common factor, difference of squares, and three-term factoring. The graphical method involves reading the x-values at the points where the graph intersects the x-axis. The video provides an example of sketching the graph of a quadratic function, emphasizing the correct shape, y-intercept, and x-intercept or points that pass through the graph.

15:03

📊 Sketching Quadratic Functions and Concept Map

This part of the script provides guidance on sketching the graph of a quadratic function, including showing the correct shape, y-intercept, and x-intercept or points that pass through the graph. Examples are given for sketching the graphs of two specific quadratic functions, detailing the steps to determine the curve's direction, axis of symmetry, y-intercept, and x-intercepts. The video concludes with a concept map summarizing the key points about quadratic functions and equations in one variable. The teacher encourages viewers to like, share, and subscribe to the channel and to comment with any questions.

Keywords

💡Quadratic Functions

Quadratic functions are mathematical functions of the form f(x) = ax^2 + bx + c, where a, b, and c are constants and 'a' is not equal to zero. These functions are fundamental in algebra and are used to model parabolic shapes. In the video, quadratic functions are introduced as a way to understand equations where the variable is squared. They are used to explain the general form of a quadratic equation and are central to the video's theme of exploring quadratic equations and their graphical representations.

💡Quadratic Equations

Quadratic equations are equations of the form ax^2 + bx + c = 0, where a, b, and c are constants, and 'a' is not zero. They represent a type of equation that can have two solutions, one solution, or no real solutions. The video script discusses how to identify quadratic expressions and equations, emphasizing that the variable's highest power must be two. Quadratic equations are integral to the video's educational content, as they are the basis for exploring the properties and solutions of quadratic functions.

💡Vertex

The vertex of a quadratic function is the point at which the parabola (graph of the quadratic function) reaches its maximum or minimum value. It is also known as the turning point or stationary point. The video explains how to find the vertex by averaging the roots for the x-value and substituting the x-value back into the function for the y-value. The vertex is a crucial concept in the video as it helps in understanding the behavior and shape of quadratic functions.

💡Axis of Symmetry

The axis of symmetry for a quadratic function is a vertical line that passes through the vertex of the parabola and divides it into two mirror-image halves. In the video, the axis of symmetry is discussed in relation to the value of 'b' in the quadratic equation, indicating its position relative to the y-axis. This concept is vital for understanding the symmetry properties of parabolas and for sketching their graphs.

💡Parabola

A parabola is the U-shaped curve that is the graph of a quadratic function. The video describes the shape of a parabola and how it resembles the letter 'U'. Parabolas are a key visual element in the video, as they help to illustrate the graphical representation of quadratic functions and equations.

💡Factorization

Factorization is a method for solving quadratic equations by expressing the quadratic expression as a product of two binomials. The video script provides examples of factorization, such as solving 4x^2 - 28x = 0 by factoring out the greatest common factor. This method is a primary focus in the video for finding the roots of quadratic equations.

💡Roots

Roots of a quadratic equation are the values of the variable that make the equation true (i.e., the solutions to the equation). The video explains how to determine if a value is a root and how to find the roots of a quadratic equation using methods like factorization. Roots are a central concept in the video as they represent the intersection points of the parabola with the x-axis.

💡Y-intercept

The y-intercept is the point where the graph of the quadratic function intersects the y-axis. It occurs when x = 0. In the video, the y-intercept is discussed in the context of sketching graphs, where the value of 'c' in the quadratic equation determines the y-intercept. This concept is important for plotting the initial point of a quadratic function on a graph.

💡X-intercept

The x-intercept, also known as the root, is the point where the graph of the quadratic function intersects the x-axis. The video explains how to find x-intercepts by setting the function equal to zero and solving for x. X-intercepts are crucial for understanding the points where the parabola touches or crosses the x-axis.

💡Coefficients

Coefficients in a quadratic equation are the numerical factors of the variables (a, b, and c in the equation ax^2 + bx + c = 0). The video discusses how the values of these coefficients affect the graph of the quadratic function, such as the direction in which the parabola opens and the position of its axis of symmetry. Coefficients are fundamental to the video's exploration of how changes in the equation affect the graphical representation.

💡Graphical Method

The graphical method is a technique for finding the roots of a quadratic equation by plotting the graph of the function and reading the x-values where the graph intersects the x-axis. The video provides an example of using the graphical method to determine the roots of a quadratic equation. This method is showcased as an alternative approach to solving quadratic equations, complementing the algebraic methods discussed.

Highlights

Quadratic functions and equations are introduced as a key topic in mathematics.

The term 'quadratic' is derived from 'quad', meaning square, due to the variable being squared.

A quadratic expression is defined as ax squared plus bx plus c.

A quadratic equation is an equation with one variable raised to the highest power of two.

The general form of a quadratic equation is ax squared plus bx plus c equals zero, where a, b, and c are constants and a cannot be zero.

Examples are provided to determine whether expressions are quadratic in one variable.

A quadratic function is represented as fx equals ax squared plus bx plus c, where a, b, and c are numbers and a is not equal to zero.

The relationship of a quadratic function is a many-to-one relation.

The graph of a quadratic function is a parabola, resembling the letter 'U'.

The vertex of a parabola is the maximum or minimum point, depending on the direction it opens.

The vertex can be found by averaging the roots and substituting the x value into the function.

The axis of symmetry is a vertical line through the vertex of the parabola.

The value of 'a' affects the direction and width of the parabola's opening.

The value of 'b' determines the position of the axis of symmetry relative to the y-axis.

The value of 'c' determines the position of the y-intercept.

A quadratic function can have up to two real roots, which are the points of intersection with the x-axis.

The roots of a quadratic equation can be found using factorization or graphing methods.

The factorization method involves setting each factor equal to zero to solve for x.

Graphical method involves reading the x values at the points of intersection with the x-axis.

The concept map of quadratic functions and equations is summarized.

Transcripts

hi i am teacher daisy

now let's learn form 4 chapter 1

quadratic functions and equations in one

variable

in this chapter you will learn 1.1

quadratic functions and equations

first we go to 1.1 quadratic functions

and equations

the name quadratic comes from quad

meaning square because the variable gets

squared

quadratic expression

ax squared plus bx plus c

quadratic equation

a quadratic equation in one variable is

an equation whereby the equation has

only one variable for example x and the

highest power for the variable is two

for example x squared

the general form of a quadratic equation

is

ax squared plus bx plus c equals zero

where a b and c are constants and a

cannot be zero

while x is the variable or unknown

for instance

in five x squared plus three x plus

three equals zero the power of two and x

squared makes it quadratic

example

determine whether each of the following

is a quadratic expression in one

variable

a two x squared plus five

b x cubed minus six

c three x squared plus two y plus one

d half m to the power of two

e two x squared minus three over x

squared

f four x squared minus

x to the power of half

solution

a yes it is a quadratic expression

b no

because the highest power of the

variable is three

see no

because there are two variables x and y

b yes it is a quadratic

expression e no

because there is a variable with a power

which is not a whole number

f no

because there is a variable with a power

which is not a whole number

quadratic function

a quadratic function is one of the form

fx equals ax squared plus bx plus c

where a b and c are numbers with a not

equal to zero

all quadratic functions have the same

image for two different objects

the type of relation of a quadratic

function is a many-to-one relation

[Music]

shape of the graph of a quadratic

function

the shape of the graph is parabola

parabolas have a shape that resembles

the letter u

maximum and minimum point of a quadratic

function

the bottom or top of the u is called the

vertex turning point or stationary point

the vertex of a parabola opening upward

is also called the minimum point if a

greater than zero

the vertex of a parabola opening

downward is also called the maximum

point if a less than zero

finding maximum and minimum points

in order to find out the x value of

vertex we add up the two roots and

divide by two

and to find out the y value of vertex

we substitute the x value into the

function

for instance consider the graph y equals

x squared minus four x

the x value of vertex equals four plus

zero divided by two

equals two

while the y value of vertex equals x

squared minus four x equals two squared

minus four times two equals negative

four

axis of symmetry of the graph of a

quadratic function

this line of axis of symmetry of

parabola is symmetric a mirror image

about a vertical line drawn through its

vertex turning point

the effects of changing the values of a

on graphs of quadratic functions

the value of a determines the shape of

the graph

if a is greater than 0 then the graph

opens upward

if a is less than zero then the graph

opens downward

the larger values of a the narrower the

graph

the smaller values of a the wider the

graph

example

state the range of values of p

explain your answer

solution

since the curve of the graph gx opens

upwards so be greater than zero

the curve of the graph gx is wider than

fx thus p less than three

therefore the range of values of p is p

is greater than zero but less than three

the effects of changing the values of b

on graphs of quadratic functions

the value of b determines the position

of the axis of symmetry

if a is more than zero

b more than zero then the axis of

symmetry lies on the left of the y-axis

b less than zero then the axis of

symmetry lies on the right of the y-axis

b equals zero then the axis of symmetry

is the y-axis

if a is less than zero

b more than 0 then the axis of symmetry

lies on the right of the y-axis

b less than 0 then the axis of symmetry

lies on the left of the y-axis

b equals 0 then the axis of symmetry is

the y-axis

if x of changing the values of c on

graphs of quadratic functions

the value of c determines the position

of the y-intercept

example

the quadratic function f x equals x

squared minus three x plus c passes

through point a negative one 3

find the value of c

solution

substitute the values of x equals

negative 1 and f x equals 3 into the

quadratic function

three equals negative one squared minus

three times negative one plus c

c equals one plus three plus c

c equals four plus c

c equals three minus four

c equals negative one

roots of a quadratic function

the roots of the quadratic equation ax

squared plus bx plus c equals zero are

the points of intersection of the graph

and the x-axis x-intercepts

it can have a maximum of two roots

the graph never touched the x-axis is

called imaginary roots

the graph touch one point in the x-axis

is called one real root

the graph touch two points in the x-axis

is called two real roots

example b

determine whether the values are roots

of the quadratic equation

two x squared minus seven x plus three

equals zero

whereby the values are x equals one and

x equals three

solution when x equals one on the left

hand side

two x squared minus seven x plus three

substitute one into x

equals two one squared minus seven one

plus three

equals two minus seven plus three

equals negative two

while the right hand side is

zero

since the left-hand side value and right

hand side value are not the same

thus x equals one is not a root of the

quadratic equation two x squared minus

seven x plus three equals zero

when x equals three on the left hand

side

two x squared minus seven x plus three

substitute three into x

equals two three squared minus seven

three plus three

equals eighteen minus twenty one plus

three

equals zero

while the right hand side is

zero

since the left hand side value and right

hand side value are the same

thus x equals three is a root of the

quadratic equation two x squared minus

seven x plus three equals zero

determine the roots of a quadratic

equation

there are four methods which are

1 factorization when possible

2. quadratic formula

3. completing the square

four graphing used to find only real

roots but in here we will only learn the

factorization method and the graphing

method

in factorization method the steps are as

follows one

express the equation in the form at x

squared plus bx plus c equals zero

two

factor the left hand side if zero is on

the right

three

set each of the two factors equal to

zero

four

solve for x to determine the roots

example determine the roots of the

following quadratic equations by

factorization method

solution

a 4x squared minus 28x equals zero

this is an example of factoring with

greatest common factor first find the

largest value which can be factored from

each term on the left side of the

quadratic equation

in this case the largest value is for x

thus for x times x minus seven equals

zero

for x equals zero or x minus seven

equals zero x equals zero or x equals

seven

therefore the roots are zero and seven

in example b x squared minus eighty one

equals zero this is an example of

factoring difference of two squares

thus x plus nine times x minus nine

equals zero

x plus nine equals zero or x minus nine

equals zero

x equals negative nine or x equals nine

therefore the roots are negative nine

and nine

in example c x squared plus 2x minus 15

equals zero

this is an example of factoring three

terms with leading coefficient of one

thus x plus five times x minus three

equals zero

[Music]

x plus five equals zero or x minus three

equals zero

x equals negative five or x equals three

therefore the roots are negative five

and three

in example d three x squared plus eleven

x minus four equals zero

this is an example of factoring three

terms with leading coefficient which is

not one

thus three x minus one times x plus four

equals zero

three x minus one equals zero or x plus

four equals zero

x equals one third or x equals negative

four

therefore the roots are one-third and

negative four

in example e 2x times x plus four equals

x minus three

in this example we will convert the

equation into the form at x squared plus

bx plus c equals zero

then solve for the value of x

two x squared plus eight x equals x

minus three

two x squared plus seven x plus three

equals zero

thus two x plus one times x plus three

equals zero

two x plus one equals zero or x plus

three equals zero

x equals negative half or x equals three

therefore the roots are negative half

and three

an example f which deals with the

proportions

x plus one divide by two equals x plus

four divide by x minus two

do the cross multiplication follows by

converting the equation

into ax squared plus bx plus c equals 0.

[Music]

2x plus 4 equals x plus one times x

minus two

two x plus eight equals x squared minus

x minus two

x squared minus three x minus ten equals

zero

x minus five times x plus two equals

zero

x minus five equals zero or x plus two

equals zero

x equals five or x equals negative two

therefore the roots are 5 and negative

2.

determine the roots of a quadratic

equation by the graphical method

read the values of x which are the

points of intersection of the graph and

the x-axis

for instance the roots are negative 1

and 3 in this diagram

example

a for the graph of quadratic equation

two x squared plus five x minus twelve

equals zero

mark and state the roots of the given

quadratic equation

the roots are negative 4 and 1.5

sketch the graph of quadratic function

the following characteristics should be

shown on the graph

1.

the correct shape of the graph

two

y-intercept

three

x-intercept or one point that passes

through the graph

example

sketch the graphs of the quadratic

functions

a f x equals x squared minus four x plus

three

b

f x equals negative two x squared plus

eighteen

solution

a f x equals x squared minus four x plus

three

value of a equals one

a greater than zero thus the curve opens

upwards

value of c equals 3 thus y-intercept

equals 3

when f x equals 0 x squared minus 4 x

plus three equals zero

factories it and become x minus three

times x minus one equals zero

x minus three equals zero or x minus one

equals zero

thus x equals three or x equals one

now we can based on the information to

sketch the graph

solution b f x equals negative two x

squared plus eighteen

value of eight equals negative two

a less than zero thus the curve opens

downwards

value of b equals zero thus axis of

symmetry is the y-axis

value of c equals eighteen

thus y-intercept equals eighteen

when f x equals zero negative two x

squared plus eighteen equals zero

simplify by dividing all the terms with

negative two

become x squared minus nine equals zero

factories it and become

x plus three times x minus three equals

zero

x plus three equals zero or x minus

three equals zero

thus x equals negative 3 or x equals 3.

now we can based on the information to

sketch the graph

the concept map of quadratic functions

and equations in one variable is as

follow

if you find this video helpful don't

forget to like share and subscribe our

channel and if you got any question can

comment below thanks for watching