Konsep Hukum Hooke | ELASTISITAS (FISIKA KELAS XI)
Summary
TLDRIn this educational video, Yusuf Ahmad explores Hooke's Law, which states that within the elastic limit, the extension of a spring is directly proportional to the force applied. He explains the mathematical representation, \( \Delta x = \frac{F}{k} \), where \( \Delta x \) is the extension, \( F \) is the force, and \( k \) is the spring constant. A practical example is given, calculating the spring constant from a spring's extension under a known load. Further, he demonstrates applying Hooke's Law to predict changes in spring extension under varying forces, emphasizing its applicability in physics.
Takeaways
- 📚 The video discusses Hooke's Law, which states that the extension of a spring is directly proportional to the force applied, as long as the elastic limit is not exceeded.
- 🔍 Hooke's Law is mathematically represented as \( \Delta x = \frac{F}{k} \) or \( F = k \cdot \Delta X \), where \( \Delta x \) is the extension of the spring, \( F \) is the force applied, and \( k \) is the spring constant.
- 📏 The spring constant \( k \) is a measure of the stiffness of the spring and is expressed in newtons per meter (N/m).
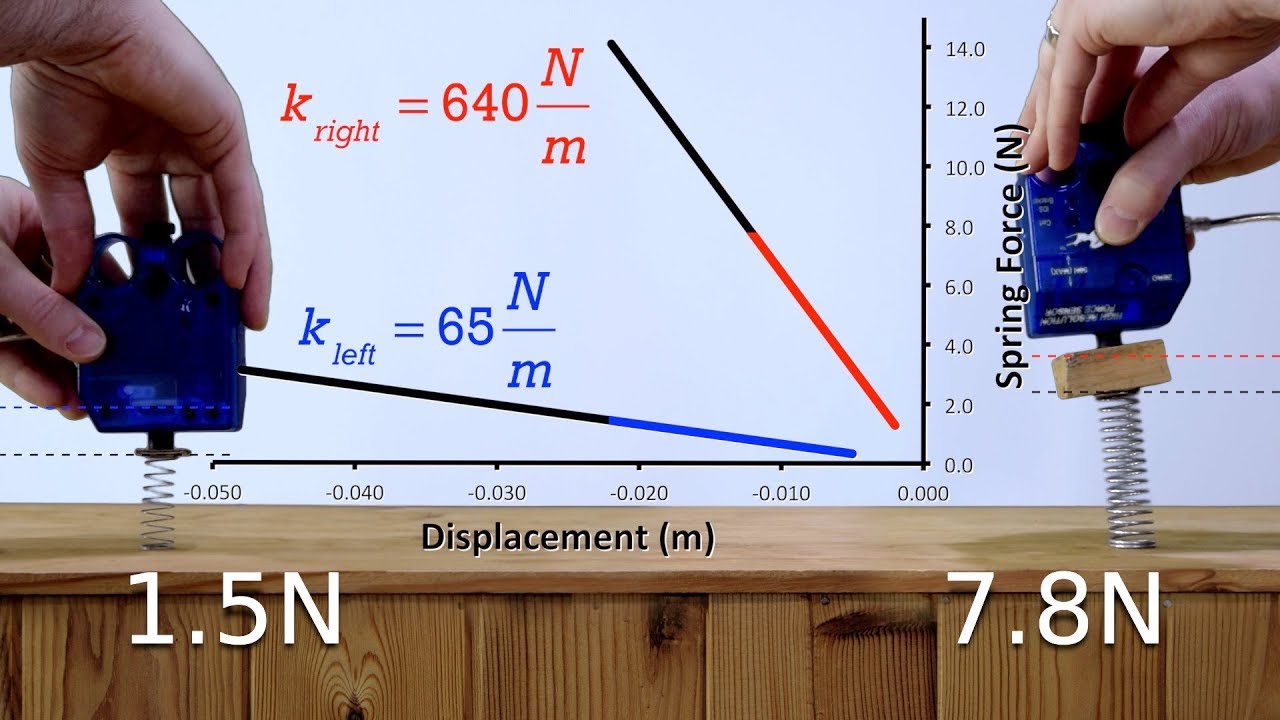
- 📈 The video provides a graphical representation showing the direct proportionality between the force applied and the extension of the spring.
- 🧐 An example problem is solved in the video, where a spring with an initial length of 15 cm extends to 19 cm under a load of 200 grams, and the spring constant is calculated.
- 🔢 The spring constant is calculated using the formula \( k = \frac{F}{\Delta X} \), and in the example, it is found to be 50 million N/m.
- 📝 Another example problem is presented where a spring extends by 2.5 cm under a force of 17.5 N, and the video explains how to predict the extension under a different force.
- 🔄 The concept of proportionality between force and extension is used to solve the second example, demonstrating the application of Hooke's Law.
- 🎓 The video concludes with a reminder to subscribe to the channel and turn on notifications for more educational content.
- 🌐 The host, Yusuf Ahmad, ends the video with a traditional greeting, emphasizing the educational and respectful nature of the content.
Q & A
What is the main topic discussed in the video by Yusuf Ahmad?
-The main topic discussed in the video is Hooke's Law, which relates to the elasticity of materials, specifically how the force applied to a spring is directly proportional to the extension or compression of the spring within its elastic limit.
What is Hooke's Law mathematically represented as?
-Hooke's Law is mathematically represented as \( \Delta x = \frac{F}{k} \) or \( F = k \cdot \Delta X \), where \( \Delta x \) is the extension or compression of the spring, \( F \) is the force applied, and \( k \) is the spring constant.
How is the spring constant (k) defined in the context of Hooke's Law?
-The spring constant (k) is defined as the force required to cause a unit extension of the spring. It is a measure of the stiffness of the spring and is expressed in newtons per meter (N/m).
What is the relationship between the force applied to a spring and its extension according to Hooke's Law?
-According to Hooke's Law, the force applied to a spring is directly proportional to its extension. This means that as the force increases, the extension of the spring also increases, and vice versa, as long as the material remains within its elastic limit.
In the example provided, what is the length of the spring before any force is applied?
-The length of the spring before any force is applied is 15 cm.
What is the extension of the spring when a 200-gram weight is applied, as mentioned in the video?
-When a 200-gram weight is applied, the extension of the spring is 4 cm, resulting in a new length of 19 cm.
How is the spring constant calculated in the example given in the video?
-In the example, the spring constant is calculated using the formula \( k = \frac{F}{\Delta x} \). With a force \( F \) of 2 N (200 grams converted to kilograms and then multiplied by the acceleration due to gravity, 10 m/s²) and an extension \( \Delta x \) of 0.04 m (4 cm in meters), the spring constant \( k \) is found to be 50 N/m.
What is the relationship between the force applied to a spring and its extension when the spring is stretched by 2.5 cm, as per the second example in the video?
-When the spring is stretched by 2.5 cm, the force applied to the spring is 17.5 N. This is consistent with Hooke's Law, which states that the force is directly proportional to the extension of the spring.
If a force of 21 N is applied to the spring that previously required 17.5 N to stretch by 2.5 cm, what is the new extension of the spring?
-Using the proportionality from Hooke's Law, if the force is increased from 17.5 N to 21 N, the new extension \( \Delta X_2 \) can be calculated as \( \Delta X_2 = \frac{21 \cdot 2.5}{17.5} \) cm, which equals 3 cm.
What is the unit of measurement for the spring constant (k) and why is it important?
-The unit of measurement for the spring constant (k) is newtons per meter (N/m). It is important because it quantifies the stiffness of the spring, indicating how much force is needed to extend or compress the spring by a certain amount, which is crucial for understanding the spring's behavior under load.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)