Equation for simple harmonic oscillators | Physics | Khan Academy
Summary
TLDRThe video explains how to represent the motion of a simple harmonic oscillator using a sine or cosine function. It demonstrates how to determine the amplitude, period, and phase shift based on the oscillator's graph. The instructor details how to write the equation for position as a function of time, taking into account amplitude (maximum displacement) and period (time for one full cycle). The video covers when to use sine, cosine, or their negative counterparts depending on the starting position of the graph, helping users understand how to model harmonic motion mathematically.
Takeaways
- 📊 The motion of a simple harmonic oscillator can be represented on a graph, with the amplitude showing the maximum displacement from equilibrium and the period indicating the time it takes to complete a cycle.
- 🌀 The equation representing a simple harmonic oscillator's motion needs to reflect the position of the mass as a function of time, either using sine or cosine functions.
- 📈 The choice between sine or cosine depends on where the graph starts. If the motion starts at a maximum, cosine is used; if it starts at zero or equilibrium, sine is used.
- ⚙️ The amplitude (A) represents the maximum displacement and scales the cosine or sine function so the oscillator reaches its actual maximum displacement.
- ⏳ The period (T) represents how long it takes for the oscillator to complete one full cycle. It is essential to adjust the equation to reflect the actual period.
- 🧮 The angular frequency (ω), which equals 2π divided by the period, ensures the function repeats correctly for any given period of the oscillator.
- 🔄 Simple harmonic motion can be visualized as circular motion on a unit circle, which helps in understanding cyclic processes in a broader context.
- 🧑🏫 To calculate the position at any given time, plug in the desired time (t) into the equation, which then returns the corresponding position value.
- 🔀 If the oscillator starts at a minimum, a negative cosine function is used; if it starts at equilibrium and goes down, a negative sine function is used.
- 📝 The equation for simple harmonic motion always follows the form: X(t) = ±Amplitude × (sine or cosine) × (2π/Period) × Time.
Q & A
What is the amplitude in the context of a simple harmonic oscillator?
-The amplitude is the maximum displacement from equilibrium in the motion of the simple harmonic oscillator. It is represented as the highest value the position graph reaches.
What is the period of a simple harmonic oscillator?
-The period (T) is the time it takes for the oscillator to complete one full cycle and return to its starting point. This can be measured from peak to peak, trough to trough, or any analogous point in the cycle.
Why is cosine used in the equation for a simple harmonic oscillator when the motion starts at a maximum?
-Cosine is used because at time t = 0, the value of cosine is 1, representing the maximum displacement of the oscillator. If the motion starts at a maximum, cosine provides the appropriate mathematical representation.
How do you modify the equation if the amplitude is not 1?
-If the amplitude is not 1, you multiply the cosine function by the amplitude (A). This ensures that the maximum displacement is correctly represented, as cosine alone only reaches a maximum of 1.
What role does the angular frequency (omega, ω) play in the equation?
-Angular frequency (ω) is used to control the period of the oscillation. It adjusts the frequency at which the motion resets, allowing the equation to reflect any period, not just the default period of 2π.
How do you adjust the equation to reflect a specific period?
-To adjust the equation for a specific period, you multiply time (t) by ω, where ω = 2π/T (T being the period). This ensures that the function resets after each period T, as desired.
Why do we use radians instead of degrees in the equation?
-Radians are used because they simplify the relationship between angular frequency and the period of the oscillator. In physics, radians are the standard for measuring angles in trigonometric functions like sine and cosine.
How does the graph of the motion change if the period increases?
-If the period increases, the graph stretches horizontally, meaning it takes more time to complete one cycle. The amplitude remains the same unless specified otherwise.
When would you use sine instead of cosine in the equation?
-Sine is used if the motion starts at zero (equilibrium) and moves up. If the motion starts at equilibrium but moves down, you would use negative sine.
How do you handle an oscillator that starts at a minimum value?
-If the motion starts at a minimum value, you use negative cosine in the equation. This reflects that the motion begins at the lowest displacement instead of the highest.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Comparing Simple Harmonic Motion(SHM) to Circular Motion - Demonstration
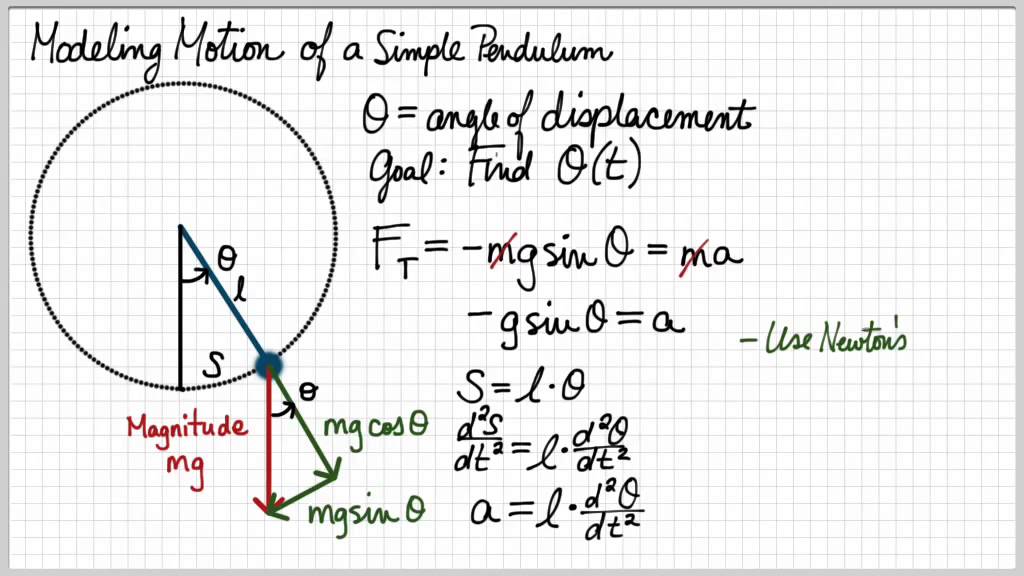
Taylor Series and Oscillating Buildings 2

Simple Harmonic Motion(SHM) - Position Equation Derivation

Movimento Harmônico Simples - Aula 02 (Força no MHS)

Media Pembelajaran Trigonometri || Jari Trigonometri (Jargonometri)
Answers for VPython - Round 1, Ep 1 Animating with Time
5.0 / 5 (0 votes)