The most beautiful idea in physics - Noether's Theorem

Summary

This script delves into Emmy Noether's groundbreaking theorem, illustrating how symmetries in a system correspond to conservation laws in physics. It explains the concept of symmetry beyond mere aesthetic appeal, extending to transformations that leave a system's energy unchanged. The video uses examples like translational and rotational symmetry to demonstrate how these symmetries imply conservation of momentum and angular momentum, respectively. It also touches on the profound implications of Noether's theorem for understanding the natural laws governing our universe, including its application in quantum mechanics.

Takeaways

• 🌌 **Symmetry in Physics**: The concept of symmetry is not just about mirror images but also includes transformations like rotation and translation that leave the system unchanged.
• 🔄 **Generalized Symmetry**: Mathematicians have generalized the concept of symmetry to include any transformation that doesn't visibly alter an object or system.
• 📚 **Importance in Mathematics**: The study of symmetry has been a driving force behind the development of abstract algebra, a significant field in modern mathematics.
• 👩‍🔬 **Emmy Noether's Theorem**: Emmy Noether's work on symmetry led to a profound theorem in physics that links symmetries to conservation laws.
• 🌀 **Symmetry Examples**: Examples of symmetries include a particle being translationally symmetric if its energy remains the same when shifted, or a rotating object being rotationally symmetric if its gravitational potential energy remains constant.
• 💡 **Conservation Laws**: Conservation laws are fundamental in physics, stating that certain quantities like momentum and energy remain constant over time if no external forces act on the system.
• 🌟 **Noether's Theorem Explained**: Noether's theorem explains the origin of conservation laws by stating that if a system is symmetric under a certain transformation, then a corresponding quantity is conserved.
• 🌍 **Universal Symmetry**: The theorem can be applied universally, from a single particle to the entire universe, to determine if certain symmetries imply conservation of specific quantities.
• 🔍 **Practical Use of Theorem**: Noether's theorem provides a method to determine what is conserved in a system by checking for symmetries, which is invaluable in solving complex physics problems.
• 🔮 **Quantum Mechanics Connection**: The concept of time translation symmetry and its relation to energy conservation is particularly important in the realm of quantum mechanics.
• 🎓 **Further Exploration**: The video encourages viewers to explore the idea of Noether's theorem further, consider its applications in different contexts, and even attempt to prove it with a background in calculus and classical physics.

Q & A

What does the thought experiment about shifting everything in the universe to the right imply?

The thought experiment suggests that if the universe could be shifted and no difference is observed, it implies a certain symmetry in the system, which according to Noether's theorem, would lead to a conservation law.

What is the significance of Emmy Noether's discovery in physics?

Emmy Noether discovered the profound idea that symmetries in a system imply conservation laws, which is a cornerstone concept in theoretical physics, linking abstract mathematical symmetries to observable physical phenomena.

How is the concept of symmetry generalized in mathematics?

In mathematics, symmetry is generalized to mean that an object remains indistinguishable under a certain transformation, such as rotation, translation, or scaling, which can be applied to a vast range of mathematical objects and structures.

What is the connection between symmetry and conservation laws as described in the script?

The connection is established through Noether's theorem, which states that for every continuous symmetry in a system, there is a corresponding conservation law. This means that the invariance of a system under certain transformations leads to the conservation of a quantity like energy, momentum, or angular momentum.

Why are conservation laws important in physics?

Conservation laws are fundamental in physics because they provide a way to predict the behavior of systems over time without the need for detailed knowledge of the system's dynamics. They simplify complex problems and are essential in both classical and quantum mechanics.

What is an example of translational symmetry given in the script?

An example of translational symmetry is a particle in isolation, where shifting its position does not change its energy, implying that the system's momentum is conserved.

How does rotational symmetry relate to the conservation of angular momentum?

According to Noether's theorem, if a system has rotational symmetry around a certain axis, then the angular momentum around that axis is conserved, as the total energy of the system remains unchanged under rotation.

What does time translation symmetry imply in the context of Noether's theorem?

Time translation symmetry implies that the energy of a system is conserved. This means if a system's energy remains the same over time, it exhibits time translation symmetry.

How does the script differentiate between systems where momentum is conserved and those where it is not?

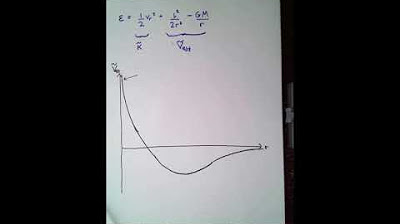
The script differentiates by examining whether the system has translational symmetry. If a system's energy changes when it is translated (e.g., due to gravitational potential energy differences), it lacks translational symmetry, and momentum is not conserved.

What is the significance of the 'homework' section at the end of the script?

The 'homework' section encourages further exploration of Noether's theorem and its implications. It prompts viewers to consider the concept's applications, explore related topics like supersymmetry, and possibly attempt to prove the theorem or identify new systems with unique symmetries.

Outlines

00:00

🌌 The Concept of Symmetry in Physics

This paragraph introduces the concept of symmetry in physics, which is not just about mirror images but also includes transformations such as rotation and translation that leave an object or system unchanged. Emmy Noether's work is highlighted, emphasizing how understanding the behavior of a system under these transformations can reveal its real behavior. The paragraph explains that symmetries imply conservation laws, a principle that Noether formalized in her theorem. The discussion includes examples of rotational and translational symmetry, and how these relate to the conservation of energy and momentum.

05:03

🔄 Noether's Theorem and Conservation Laws

The second paragraph delves into Noether's theorem, which connects symmetries in a system to the conservation laws that govern it. It explains that if a system is symmetric under a certain transformation, such as translation or rotation, then a corresponding physical quantity, like momentum or angular momentum, is conserved. The paragraph uses examples to illustrate this concept, such as a particle in free space or a system affected by gravity, to show how the presence or absence of symmetry leads to conservation or non-conservation of physical quantities. It also touches on the idea of time translation symmetry and its relation to the conservation of energy, setting the stage for its importance in quantum mechanics.

Keywords

💡Symmetry

Symmetry in the context of the video refers to the property of a system that remains unchanged under certain transformations. It's a fundamental concept in physics and mathematics, where it's used to describe situations where an object or system looks the same or behaves the same after a transformation like rotation, translation, or reflection. The video explains that symmetries can be more abstract than just mirror images, and they can be used to understand the behavior of physical systems. For instance, rotational symmetry in the orbit of a planet around a star implies that the gravitational potential energy remains the same, which is a key point in Noether's theorem.

💡Transformation

A transformation in this video script is an operation applied to a system that might change its state or position but not its fundamental properties. Examples include rotating, translating, or stretching a system. The video discusses how transformations are used to test for symmetries, such as checking if a system's energy remains the same after it has been translated, which would indicate translational symmetry.

💡Conservation Laws

Conservation laws are principles in physics that state certain quantities, like energy, momentum, or angular momentum, do not change in an isolated system. The video script explains that these laws are not arbitrary but are deeply connected to the symmetries of the system. For example, if a system is symmetric under translation (it looks the same no matter where you place it), then its momentum is conserved according to Noether's theorem.

💡Emmy Noether

Emmy Noether was a German mathematician who made significant contributions to the field of theoretical physics and abstract algebra. The video highlights her theorem, which links symmetries in physical systems to conservation laws. Noether's work is foundational in understanding why certain quantities are conserved in nature, such as momentum and energy, and her theorem provides a mathematical framework for predicting which quantities will be conserved given a system's symmetries.

💡Abstract Algebra

Abstract algebra is a branch of mathematics that studies algebraic structures like groups, rings, and fields in an abstract way, without necessarily referring to their numeric or geometric properties. The video mentions that the study of symmetry was a motivation for the development of abstract algebra, and Emmy Noether was an expert in this field. Her work on symmetries and their mathematical generalizations laid the groundwork for understanding the deep connections between symmetries and conservation laws in physics.

💡Translational Symmetry

Translational symmetry refers to the property of a system that remains unchanged when it is moved in space. In the video, this concept is used to explain how the conservation of momentum is related to the system's symmetry under translation. If moving a system up or down by a certain amount lambda does not change its total energy, then the system is said to have translational symmetry, and according to Noether's theorem, its momentum is conserved.

💡Rotational Symmetry

Rotational symmetry is a type of symmetry where a system looks the same after being rotated by a certain angle. The video uses the example of an object orbiting in a circle to illustrate rotational symmetry. If the gravitational potential energy of the object remains the same after it is rotated, then the system has rotational symmetry, and Noether's theorem implies that its angular momentum is conserved.

💡Gravitational Potential Energy

Gravitational potential energy is the energy an object possesses because of its position in a gravitational field. In the video, it is used to explain how the presence or absence of certain symmetries can affect the conservation of energy. For example, if moving an object closer to a planet changes its gravitational potential energy, then the system does not have translational symmetry, and momentum is not conserved.

💡Angular Momentum

Angular momentum is a measure of the rotational motion of an object and is conserved in systems that have rotational symmetry. The video explains that if a system is symmetric under rotations around a particular axis, then the angular momentum around that axis is conserved. This is a direct consequence of Noether's theorem, which connects symmetries to conservation laws.

💡Time Translation Symmetry

Time translation symmetry is a concept where a system's energy remains the same when compared at different times. The video mentions that if a system is symmetric under time translations, then energy is conserved. This is a less intuitive concept than spatial symmetries but is crucial for understanding conservation laws in quantum mechanics, as hinted at in the script.

Highlights

Emmy Noether's theorem is introduced as a profound idea in physics that connects symmetries to conservation laws.

Symmetry is generalized beyond just mirror images to include transformations that leave an object indistinguishable.

Rotational and translational symmetries are explained with examples to illustrate their relevance in physics.

The importance of symmetries in mathematics and their role in abstract algebra is discussed.

Noether's theorem is explained through the lens of energy conservation in systems under transformation.

Translational symmetry is exemplified by a particle in isolation and its conservation of momentum.

The gravitational influence on a system's symmetry and energy is used to explain why certain systems are not translationally symmetric.

Rotational symmetry of an orbiting object and its conservation of angular momentum are discussed.

Conservation laws are emphasized as essential tools in physics, simplifying complex problems.

Noether's theorem is praised for providing a deeper understanding of why conservation laws exist.

The example of a ball rolling on the ground is used to illustrate the non-conservation of momentum in certain systems.

The concept of time translation symmetry and its connection to energy conservation is introduced.

Noether's theorem is described as a method to mathematically derive conservation laws from symmetries.

The reciprocal nature of Noether's theorem allows for the identification of symmetries from conserved quantities.

The philosophical and aesthetic appeal of symmetries and their natural connection to conservation laws is discussed.

Homework is suggested to explore the concept of Noether's theorem further, including its application in quantum mechanics.

The video challenges viewers to think about systems with unique symmetries and to predict what might be conserved in those systems.

Transcripts

What if everything in the universe was actually a bit to the right of where it is now?

Or if this orbiting planet was actually half a rotation ahead?

What changes?

More importantly what stays the same?

These seem like fun but useless thought experiments until Emmy Noether discovered, what I think,

is the most profound and far-reaching idea in physics.

Knowing what happens to a system under these imaginary transformations, gives us insight

into the systems real behaviour.

The usual summary is: symmetries imply conservation laws.

In this video, I’ll explain what that means.

We’ll start with symmetry.

Normally we use the word symmetry to mean that if we took the mirror image along some

line, a symmetric object looks the same.

Mirror symmetries are pretty, but we can make the word symmetry mean so much more.

For example rotational symmetry: when you can rotate an object a certain amount and

it looks just the same as before, or another example is translational symmetry.

In fact mathemations took the idea of symmetry and generalised it completely.

a symmetry is anything where you have some sort of object and apply some sort of transformation

to it, and you can’t tell the difference- in some sense.

This might seem like they’ve taken a good descriptive word and then generalized it till

it’s meaningless.

But actually this idea is very useful.

These abstract symmetries are a constantly reoccurring theme in mathematics - in fact,

the study symmetry helped motivate a one of the most important fields of modern mathematics

called abstract algebra.

Emmy Noether was an expert in symmetry, developing foundational concepts in abstract algebra.

It was during a small pause from her extremely influential mathematical career that she thought

about physics.

She wondered if she could apply the idea of symmetry to the world, and that’s what lead

to her beautiful theorem.

This is the symmetry that she considered.

The object is some system, a part of the universe.

It could be a thing someone is throwing.

Or a particle in a void.

Or maybe some binary stars.

Or if you want, the whole universe.

Then you transform it.

For example, you could rotate it by some angle lambda.

Or shift it up or down by lambda, or stretch all the distances by lambda.

Now we’re interested in if the system is ‘the same’ in some sense.

Noether decided the interesting thing to check is if the total energy of the objects would

be the same.

So we say that a system has a symmetry under a transform if the total energy of the objects

didn’t change.

For example, if I had a particle all by itself and then compared it to a shifted version,

clearly the energy is the same.

So this system is translationally symmetric.

On the other hand, say there was a big planet near by.

A particle that is closer has got more gravitational potential energy, so this isn’t translationally

symmetric.

Or consider this object orbiting in a circle, and compare it to a rotated version.

Both objects are an equal distance from the planet and so both ways, they have the same

gravitational potential energy.

So this system is rotationally symmetric.

So that’s the symmetry part of Noether’s theorem.

Now let’s look at conservations.

If you’ve ever studied physics, for example at school, you’ll know how important these

things called conservation laws are.

It means that if you have a bunch of things and you counted up their total momentum let’s

say, then you let them go for any amount of time and counted the momentum again, it would

be the same number.

Technically, you can do physics without ever needing to use these conservation laws.

But.

Often they’ll give you some insane problem that looks like you shouldn’t be able to

solve- at least not easily...

But if you invoke the magical conservation laws your answer just falls out.

Conservations laws aren’t just useful for classical physics either, they help out in

quantum mechanics and really all of modern physics.

I used to not like using conservation laws because they can make it seem too easy.

As in, I’d get the solution with so little work that it really feels like magic and so

I didn’t feel like I understood why it worked.

After all, I didn’t understand why energy is conserved or why momentum is conserved,

so if I used one of those to solve a problem then clearly I didn’t understand the solution

Noether’s theorem is powerful because it explains where conservations come from.

Let me go back to an example.

I said that momentum is conserved.

But this, is kind of not true not always true.

If I choose my system to be a ball rolling on the ground, we all know that eventually

it stops.

Or if I dropped something, it gets faster and faster.

Sure, if you take everything as your system momentum is always conserved, but how can

I know whether a particular system’s momentum won’t change.

Noether’s theorem gives us a simple way to know, regardless of whether the system

is one particle or the whole universe.

She proved that you only get conservations if the system has the right symmetries.

Again, let’s look at examples.

If you have translational symmetry, the theorem says you have conservation of momentum.

We know that a particle that’s on its own has this symmetry, so it’s momentum is conserved.

That’s true, it will continue on at the same speed in the same direction forever.

If we instead had a bunch of particles by themselves as our system, this system is also

translationally symmetric-if they all over there instead, that doesn’t change their

energy.

So again, Noether tells us we have conservation of their total momentum, which wouldn’t

be that obvious otherwise.

In fact, if we consider a shifted version of the universe, no one would be able to tell

the difference and so there’s no difference in the energy.

Hence the momentum of the universe is conserved.

When isn’t momentum conserved for a system?

What about this object that gains speed as it falls?

Noether’s theorem says that this system can’t have translational symmetry, so let’s

check.

What if this object was nearer to the ground?

It would have had less gravitational potential energy- Good!

It isn’t symmetric.

How about rotational symmetry?

Like we said, this object could have been rotated here and the energy wouldn’t change,

so it has rotational symmetry around this axis.

We also know it has angular momentum in this direction, and that it goes at the same speed

the whole way, so its angular momentum is conserved.

And this is what noether’s theorem predicts, if you have rotational symmetry around one

axis, then the angular momentum in that direction is conserved.

One last example, this one is a weird one.

We’ve talked about translating in space and in angle, but what about translating in

time?

In otherwords, you have a system doing something at the moment and you compare it to the same

system some time later.

If it has the same energy then it is time translation symmetric.

What does Noether say is conserved then?

It’s energy.

I know, that’s a bit circular here, but it is more important when we come to quantum

mechanics- so I had to mention it.

Noether didn’t just come up with these three examples.

Instead, she gave us a mathematical way to turn any symmetry into a conservation and

vis versa.

See these conserved quantities are called the generators of these transformations and

you can calculate what the generator is for any transformation you come up with.

If I encountered some exotic system and noticed it is symmetric under a transformation, there

is a mathematical way for me to calculate what’s conserved.

There’s also the converse.

Say I notice noticed that some mysterious new quantity

is conserved.

Noether’s theorem says that conservation is from some symmetry, and the conserved quantity

is the generator of the transformation, so I can calculate which transformation it is.

That’s very powerful, but the theorem is amazing because it is just as beautiful and

it is useful.

Symmetries appeal to us, and seem natural.

We think it makes sense that if the universe was shifted, or rotated that nothing should

change, there’s no difference between here and there.

So showing that symmetry and conservation laws are equivalent shows that conservation

laws must be just as natural.

Homework Let me know what you think of this idea.

Have you heard of it before?

Maybe you’ve heard about things like super symmetry in physics- try find out how that’s

related.

The version of Noether’s theorem I talked about here is the one for classical physics

(including GR), only its much less powerful version of the theorem than she created (but

I don’t understand that one so...).

If you know some calculus and classical physics, try and find a proof of this theorem.

And this is a fun activity, try come up with strange systems with strange symmetries- then

see if you can figure out what’s conserved.