Population vs Sample
Summary
TLDRThis video script introduces the fundamental concepts of population and sample in statistical analysis. It explains that a population encompasses all items of interest, while a sample is a subset used due to practical constraints like time and cost. The script highlights the importance of random and representative sampling to ensure the sample accurately reflects the population. It uses the example of surveying New York University students to illustrate these points and emphasizes that while sampling can be challenging, statistical tests are designed to work with such data, making minor sampling errors less critical.
Takeaways
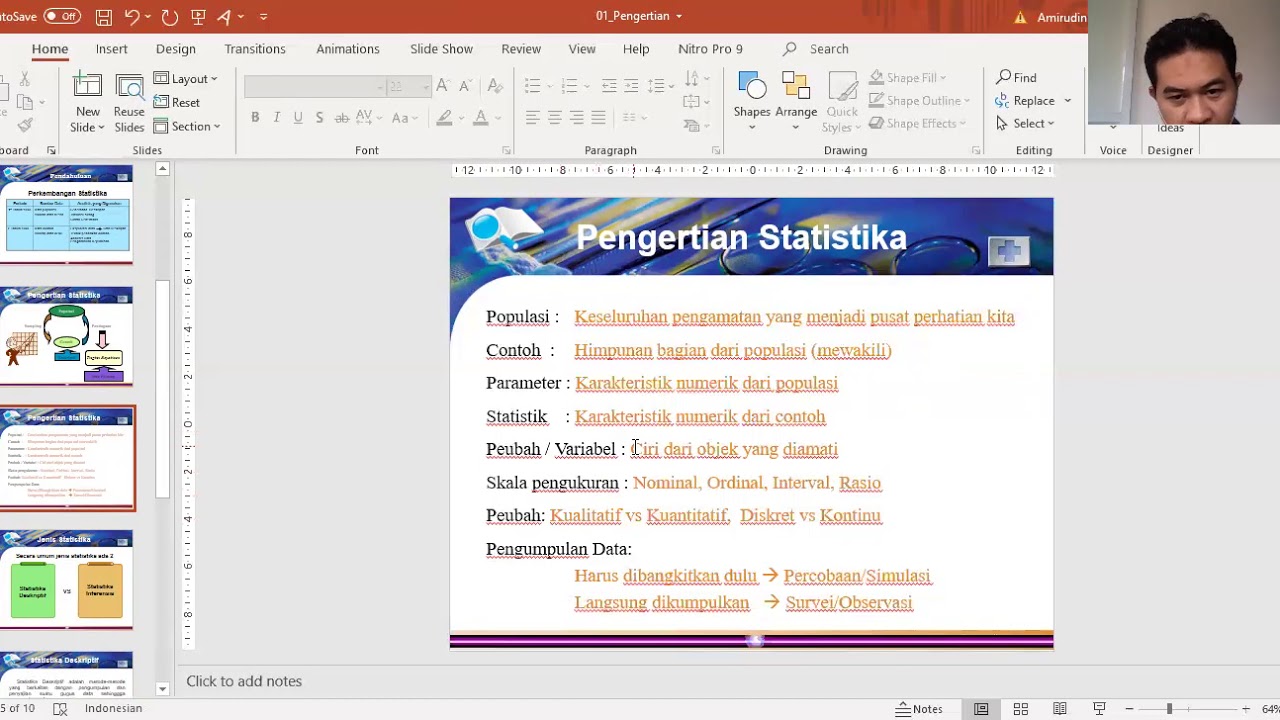
- 📚 The first step in statistical analysis is to determine if the data is a population (all items of interest) or a sample (subset of the population).
- 🔢 Parameters are the numbers obtained from a population, while statistics are derived from samples.
- 🏛️ The population for a study can be extensive and include various groups such as on-campus, distance education, and part-time students.
- 🕵️♂️ A sample should ideally be easy to contact, less time-consuming, and less costly to gather compared to a whole population.
- 📈 Random sampling ensures that each member of the population has an equal chance of being selected for the sample.
- 🍽️ The example of interviewing students in the university canteen is highlighted as a non-random and non-representative sampling method.
- 🎯 Representativeness in a sample means it accurately reflects the characteristics of the entire population.
- 📊 A truly representative sample for NYU students would require random selection from a comprehensive student database.
- 🔎 Recognizing representative samples becomes easier with experience, and minor sampling errors are often manageable with statistical tests.
- 🎓 The course aims to make understanding populations and samples, as well as the nuances of sampling, straightforward for the learners.
Q & A
What is the difference between a population and a sample in statistical analysis?
-A population is the complete collection of all items of interest in a study, denoted by uppercase N, while a sample is a subset of the population, denoted by lowercase n.
Why are parameters and statistics important in statistics?
-Parameters are the numbers obtained from a population and represent the true values of the population. Statistics are the numbers obtained from a sample and are used to estimate the parameters.
What is the population in the context of a survey about job prospects at New York University?
-The population includes all students studying at New York University, including those on campus, at home, on exchange, abroad, in distance education, part-time students, and even those who are enrolled but still at high school.
Why is it challenging to define and observe a population in real life?
-Populations are hard to define and observe because they can include a vast and diverse group of individuals that may be spread across different locations and situations.
What are the advantages of using a sample over analyzing an entire population?
-Sampling is less time-consuming and less costly compared to analyzing an entire population. It allows for more manageable and feasible data collection within limited resources.
Why might interviewing 50 students in the NYU canteen not provide a true representation of the whole university?
-The sample is neither random nor representative because the students were not chosen by chance and only represent those who were present at the canteen during lunchtime.
What is a random sample, and why is it important?
-A random sample is one where each member is chosen from the population by chance, ensuring each member has an equal likelihood of being selected. This is important for ensuring that the sample is unbiased and can accurately represent the population.
What is a representative sample, and how does it reflect the population?
-A representative sample is a subset of the population that accurately reflects the characteristics of the entire population. It should include a diverse mix of individuals that mirrors the population's demographics and other relevant attributes.
How can one ensure a sample is both random and representative?
-Ensuring a sample is both random and representative can be achieved by using a random selection method, such as accessing a complete database and selecting individuals at random, which helps in capturing the diversity of the population.
What are the two big advantages of using samples in statistical analysis despite the challenges?
-The two advantages are that with experience, it becomes easier to recognize a representative sample, and statistical tests are designed to work with incomplete data, making small sampling errors less critical.
What is the role of statistical tests when working with samples?
-Statistical tests help in analyzing and interpreting data from samples to make inferences about the population. They account for the variability and incompleteness of sample data, allowing for robust conclusions despite potential sampling errors.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)