Ángulo doble: problemas de trigonometría
Summary
TLDREn este vídeo de unprofesor.com, se explica el concepto de ángulo doble en trigonometría. Se presentan fórmulas clave como el seno, coseno y tangente de un ángulo doble, ejemplificando con el ángulo de 30 grados para obtener los valores correspondientes de 60 grados. Se resuelven problemas prácticos para entender cómo aplicar estas fórmulas, como calcular el seno, coseno y tangente de 120 grados, utilizando el seno y coseno de 60 grados. El vídeo es una herramienta valiosa para estudiantes que buscan comprender y practicar trigonometría.
Takeaways
- 🔢 El ángulo doble de 30 grados es 60 grados.
- 📐 La fórmula del seno de un ángulo doble es 2 * sen(a) * cos(a).
- 📏 La fórmula del coseno de un ángulo doble es cos^2(a) - sen^2(a).
- 📈 La fórmula de la tangente de un ángulo doble es 2 * tan(a) / (1 - tan^2(a)).
- 📘 Se aclara que tan^2(a) no se interpreta como dos veces la tangente de a, sino como la tangente de a al cuadrado.
- 📌 Las fórmulas de ángulo doble no necesariamente deben memorizarse, ya que se pueden encontrar en un formulario.
- 📐 Se aplica la fórmula del seno de un ángulo doble para calcular sen(120°) como 2 * sen(60°) * cos(60°).
- 📏 Se calcula el coseno de 120° usando la fórmula cos^2(60°) - sen^2(60°).
- 📈 Se resuelve la tangente de 120° con la fórmula 2 * tan(60°) / (1 - tan^2(60°)), resultando en -√3.
- 💡 Se enfatiza la importancia de aplicar las fórmulas de ángulo doble en problemas de trigonometría y la utilidad de recordarlas para exámenes.
Q & A
¿Qué es el ángulo doble en trigonometría?
-El ángulo doble se refiere a un ángulo que es el doble de otro ángulo dado, por ejemplo, si el ángulo es de 30 grados, el ángulo doble sería de 60 grados.
¿Cómo se calcula el seno de un ángulo doble?
-El seno de un ángulo doble (2a) se calcula como 2 * sen(a) * cos(a), donde 'a' es el ángulo original.
¿Cuál es la fórmula para el coseno de un ángulo doble?
-El coseno de un ángulo doble (2a) se calcula como el coseno al cuadrado de 'a' menos el seno al cuadrado de 'a', es decir, cos²(a) - sen²(a).
¿Cómo se determina la tangente de un ángulo doble?
-La tangente de un ángulo doble (2a) se calcula como 2 * tan(a) dividido entre 1 - tan²(a).
¿Por qué es importante recordar las fórmulas de ángulo doble en trigonometría?
-Es importante recordar las fórmulas de ángulo doble porque permiten resolver problemas trigonométricos más complejos y son útiles en situaciones donde se requiere calcular el seno, coseno o tangente de un ángulo que es el doble de otro ángulo conocido.
¿Qué pasa si se confunde la fórmula de tangente de ángulo doble con la de ángulo simple?
-Confundir la fórmula de tangente de ángulo doble con la de ángulo simple puede llevar a resultados incorrectos en los cálculos, ya que la fórmula de ángulo doble es 2 * tan(a) / (1 - tan²(a)), mientras que la de ángulo simple es simplemente tan(a).
¿Cómo se calcula el seno de 120 grados usando la fórmula de ángulo doble?
-El seno de 120 grados se calcula como 2 * sen(60) * cos(60), lo que da como resultado 2 * (√3 / 2) * (1 / 2), que es igual a √3.
¿Cuál es el resultado del coseno de 120 grados según la fórmula de ángulo doble?
-El coseno de 120 grados se calcula como cos²(60) - sen²(60), que es (1/2)² - (√3 / 2)², y resulta en -1/2.
¿Cómo se determina la tangente de 120 grados utilizando la fórmula de ángulo doble?
-La tangente de 120 grados se calcula como 2 * tan(60) / (1 - tan²(60)), que es 2 * (√3) / (1 - 3), y resulta en -√3.
¿Cuáles son otras fórmulas trigonométricas que son útiles además de las de ángulo doble?
-Además de las fórmulas de ángulo doble, también son útiles las fórmulas para el ángulo mitad, la suma y la resta de ángulos, que son necesarias para resolver problemas trigonométricos más variados.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
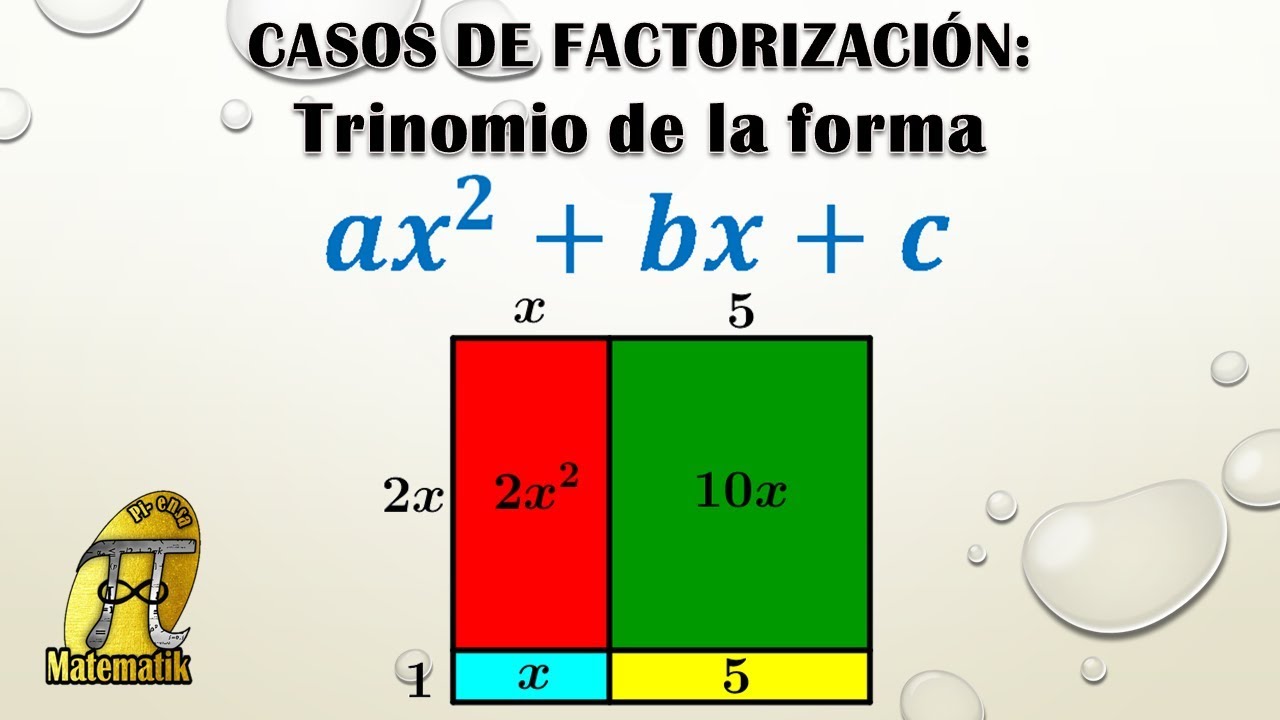
Trinomio de la forma ax^2+bx+c gráficamente | Casos de Factorización

Primer Condicional En Ingles - Oraciones Con First Conditional – Negativas Interrogativas

Consultas en MongoDB con Compass (con ejemplos)

✅ La GUERRA DE LOS SEIS DÍAS en 10 minutos | Israel contra Egipto, Jordania y Siria

DETERMINACIÓN GRAVIMÉTRICA DE HIERRO III COMO ÓXIDO FÉRRICO, PARTE I PRECIPITACIÓN

EL RETÍCULO ENDOPLASMATICO RUGOSO Y LISO en 5 minutos. Funciones del retículo endoplasmático. Fácil

¿Qué es el INDAUTOR?
5.0 / 5 (0 votes)
