77. OCR A Level (H046-H446) SLR13 - 1.4 Hexadecimal representation
Summary
TLDRThis video tutorial focuses on representing positive integers in hexadecimal, a base 16 number system. It explains how hexadecimal uses 16 unique digits, including the letters A-F to represent values 10-15. The video compares hexadecimal with binary and decimal systems, highlighting hexadecimal's utility in computer science for compactly representing large binary numbers, colors, and memory addresses. It also touches on the historical use of other base number systems like base 20 by Mayans and base 60 by Babylonians.
Takeaways
- 🔢 Hexadecimal is a base 16 number system, utilizing 16 unique digits to represent values from 0 to 15.
- 🆎 In hexadecimal, the digits 10 to 15 are represented by the letters A through F, with A corresponding to 10 in decimal.
- 🔄 The video emphasizes the close relationship between hexadecimal and binary, where each hexadecimal digit directly corresponds to a 4-bit binary sequence.
- 💡 Hexadecimal is particularly useful in computer science for representing large binary numbers in a more compact form.
- 🖥️ Computers use hexadecimal to represent various data types such as colors, memory addresses, and MAC addresses due to its efficiency and readability.
- 🌐 The video script provides a side-by-side comparison of base 10 (decimal), base 16 (hexadecimal), and base 2 (binary) number systems, illustrating how they represent numbers from 0 to 15.
- 📈 The script explains how hexadecimal simplifies the representation of binary numbers, allowing for easier understanding and manipulation of binary data.
- 📝 The video encourages viewers to explore the provided table to understand the relationship between binary nibbles and hexadecimal digits.
- 🎓 For exams, understanding how to represent positive integers in hexadecimal and recognizing the utility of hexadecimal in representing large binary numbers is crucial.
- 🌟 The video concludes with a brief historical overview of other base number systems, such as base 20 used by the Mayans and base 60 used by the Babylonians.
Q & A
What is the base of the hexadecimal number system?
-The hexadecimal number system is base 16.
How does the hexadecimal system represent values 10 to 15?
-In hexadecimal, values 10 to 15 are represented by the letters A through F, respectively.
What is the significance of the hexadecimal system in computer science?
-Hexadecimal is significant in computer science because of its close relationship with binary, making it useful for representing large binary numbers in a more compact form.
Why is hexadecimal preferred over binary for certain applications?
-Hexadecimal is preferred over binary for certain applications because it allows for a more concise representation of large binary numbers, making it easier to read and work with.
What are some common uses of hexadecimal in computing?
-Hexadecimal is used in computing to represent colors, memory addresses, MAC addresses, and much more.
How can hexadecimal be used to represent positive integers?
-Hexadecimal can represent positive integers by using 16 unique digits, from 0 to 9 and A to F, to represent values from 0 to 15.
What is a nibble in the context of hexadecimal and binary?
-A nibble is a group of four binary digits (bits), which can be represented by a single hexadecimal digit.
How does the hexadecimal system compare to the decimal and binary systems?
-The hexadecimal system, like decimal and binary, can represent the numbers 0 and 1 with a single digit. However, for numbers 2 through 9, it uses the same digits as decimal, and for 10 through 15, it uses the letters A through F.
What are the three base number systems mentioned in the script?
-The three base number systems mentioned in the script are base 2 (binary), base 10 (decimal), and base 16 (hexadecimal).
Can you provide an example of how hexadecimal simplifies binary representation?
-For example, the binary sequence 1100 0010 can be simplified to the hexadecimal number C2, making it more compact and easier to read.
Are there other base number systems that have been used historically?
-Yes, throughout history, other base number systems have been used, such as the Mayans' base 20 system and the Babylonians' base 60 system.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

VLSI.4.5.Octal and Hexadecimal Number System

Konversi Bilangan Heksadesimal menjadi Bilangan Biner

78. OCR A Level (H046-H446) SLR13 - 1.4 Converting between binary, hex & denary

Konversi Bilangan Hexadesimal ke Basis Bilangan Yang Lain
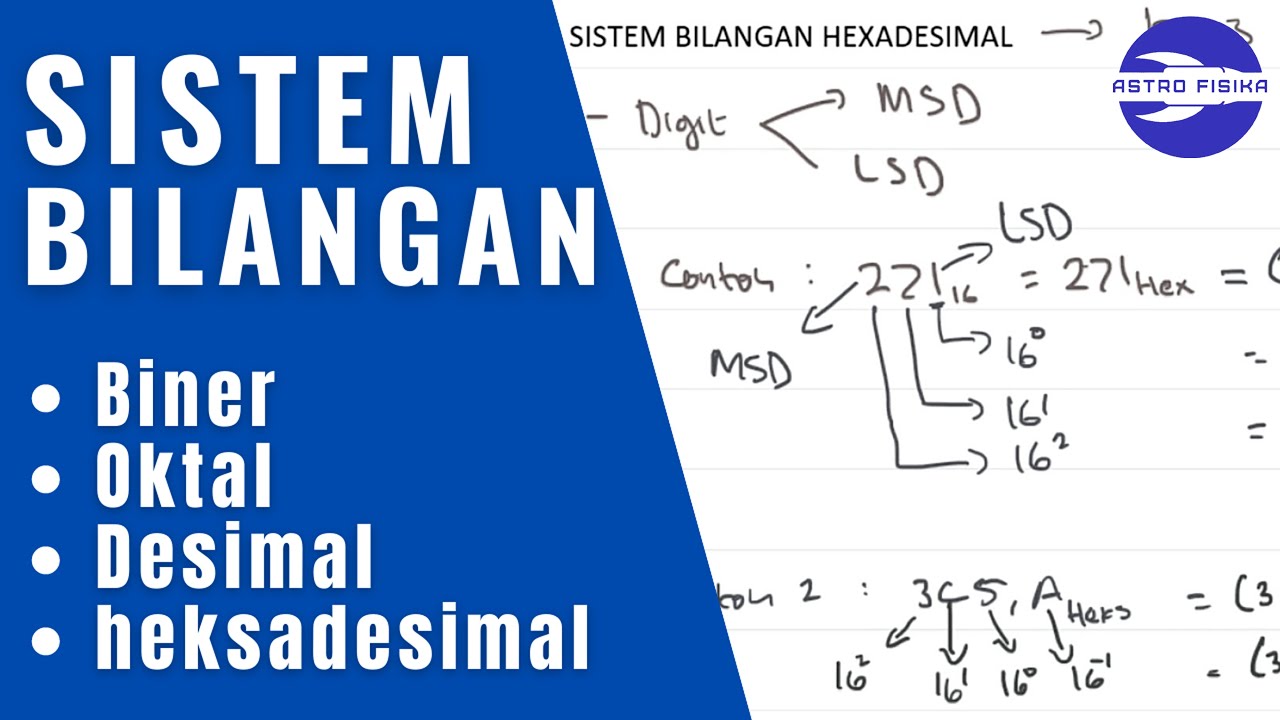
ELEKTRONIKA DIGITAL: SISTEM BILANGAN (Biner, Oktal, Desimal, Heksadesimal)

ED2. Sistemi di Numerazione
5.0 / 5 (0 votes)