15. Integral de raíz cuadrada en el denominador (Exponente negativo y fraccionario)
Summary
TLDREn este segmento del curso de integrales, se explica cómo integrar la función '3 dividido entre la raíz cuadrada de x'. Se utiliza la propiedad de la raíz cuadrada como potencia fraccionaria, se simplifica la fracción cambiando el signo del exponente y se extrae la constante 3 fuera de la integral. Luego, se aplica la fórmula de integración para potencias, resultando en '3x al medio'. Seguidamente, se divide el resultado utilizando la regla de la herradura, lo que lleva a la simplificación final. El video invita a los estudiantes a intentar integrar un polinomio y promete mostrar el procedimiento en el próximo episodio.
Takeaways
- 📘 El curso trata sobre integrales y en esta lección se aborda la integración de la función '3 dividido entre raíz cuadrada de x'.
- 🔢 Se utiliza la propiedad de que la raíz cuadrada de x es equivalente a x elevado a la potencia de 1/2.
- ✏️ Se aplica una propiedad algebraica para mover una potencia del denominador al numerador, cambiando el signo del exponente.
- 📐 Se simplifica la fracción eliminando la raíz cuadrada en el denominador.
- 🔑 Se extrae la constante '3' fuera de la integral, simplificando la integración.
- 🧮 Se utiliza la fórmula de integración para potencias, sumando 1 al exponente y dividiendo entre el nuevo exponente.
- 📉 Se realiza una operación algebraica para simplificar la potencia resultante, obteniendo x elevado a la potencia de 1/2.
- 🛠 Se aplica la regla de la herradura para dividir fracciones, multiplicando el numerador por el denominador invertido.
- 📌 Se simplifica el resultado final, regresando a la notación de raíz cuadrada para la respuesta final.
- 📚 Se invita a los estudiantes a intentar integrar un polinomio utilizando las propiedades de integrales vistas en la lección.
Q & A
¿Qué método se utiliza para integrar la función 'tres dividido entre la raíz cuadrada de x'?
-Se utiliza la propiedad de que la raíz cuadrada de x es igual a x elevado a la potencia de 1/2, y luego se aplica la propiedad de la integral para poder mover una potencia del denominador al numerador cambiando el signo del exponente.
¿Cuál es el resultado de integrar '3/(x^(1/2))' utilizando la propiedad mencionada en el guion?
-El resultado es 3x^(1/2) dividido entre 1/2, es decir, 6x^(1/2).
¿Qué es la 'regla de la herradura' y cómo se aplica en el caso de la integral '3/(x^(1/2))'?
-La 'regla de la herradura' es una técnica para simplificar divisiones que involucran fracciones. Se aplica multiplicando el numerador y el denominador entre sí. En este caso, se convierte la expresión en una fracción y se multiplica el numerador (3x^(1/2)) por el denominador invertido (1/(1/2)), resultando en 6x^(1/2).
¿Cómo se calcula la integral de una suma o resta de funciones?
-La integral de una suma o resta de funciones se puede separar como la integral de cada término por separado, es decir, la integral de la suma es la suma de las integrales de los términos individuales.
¿Qué pasos se sugieren para integrar un polinomio en el siguiente vídeo?
-Se sugiere integrar cada término del polinomio por separado: primero la integral de 5x al cubo, luego la integral de 7x al cuadrado, después la integral de -5x y finalmente la integral de -4.
¿Cuál es la fórmula general para integrar una potencia de x, como se menciona en el guion?
-La fórmula general para integrar una potencia de x es sumar 1 al exponente del x y dividir entre el nuevo exponente, es decir, ∫x^n dx = (x^(n+1))/(n+1) + C, donde C es la constante de integración.
¿Qué significa 'x elevado a la un medio' en términos de potencias?
-'X elevado a la un medio' es la misma expresión que 'raíz cuadrada de x', que se escribe como x^(1/2).
¿Qué es la constante que se menciona en el guion y cómo se maneja en la integral?
-La constante mencionada en el guion es el número 3, que se maneja al salir de la integral, dejando la integral de x^(-1/2) multiplicada por 3.
¿Cómo se simplifica la fracción que resulta de la integral '3/(x^(1/2))'?
-Se simplifica aplicando la regla de la herradura, convirtiendo la fracción en su forma inversa y multiplicando los términos correspondientes, lo que resulta en 6x^(1/2).
¿Cuál es la importancia de la propiedad de la integral que permite mover una potencia del denominador al numerador?
-Esta propiedad es importante porque permite simplificar integrales que involucran fracciones con potencias en el denominador, facilitando el proceso de integración.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

12. Integral de raiz de 3 por equis cuadrada

06. Integral de una potencia de x (x a la quinta)

06. Valor de una función con raíz cuadrada

04. Integral de una constante (Raíz cuadrada)
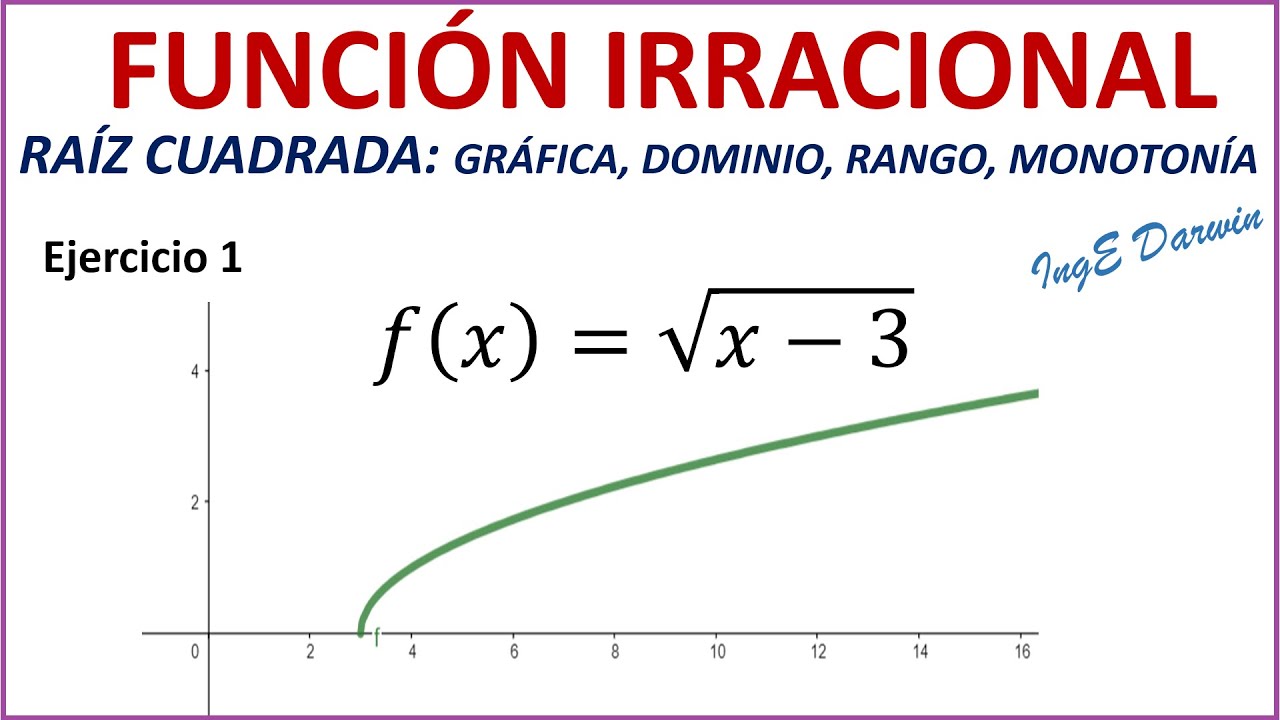
FUNCIÓN RAÍZ CUADRADA: Gráfica, Dominio, Rango y Monotonía - Explicación detallada | Ejercicio 1

Integral de una raíz | Ejemplo 1
5.0 / 5 (0 votes)
