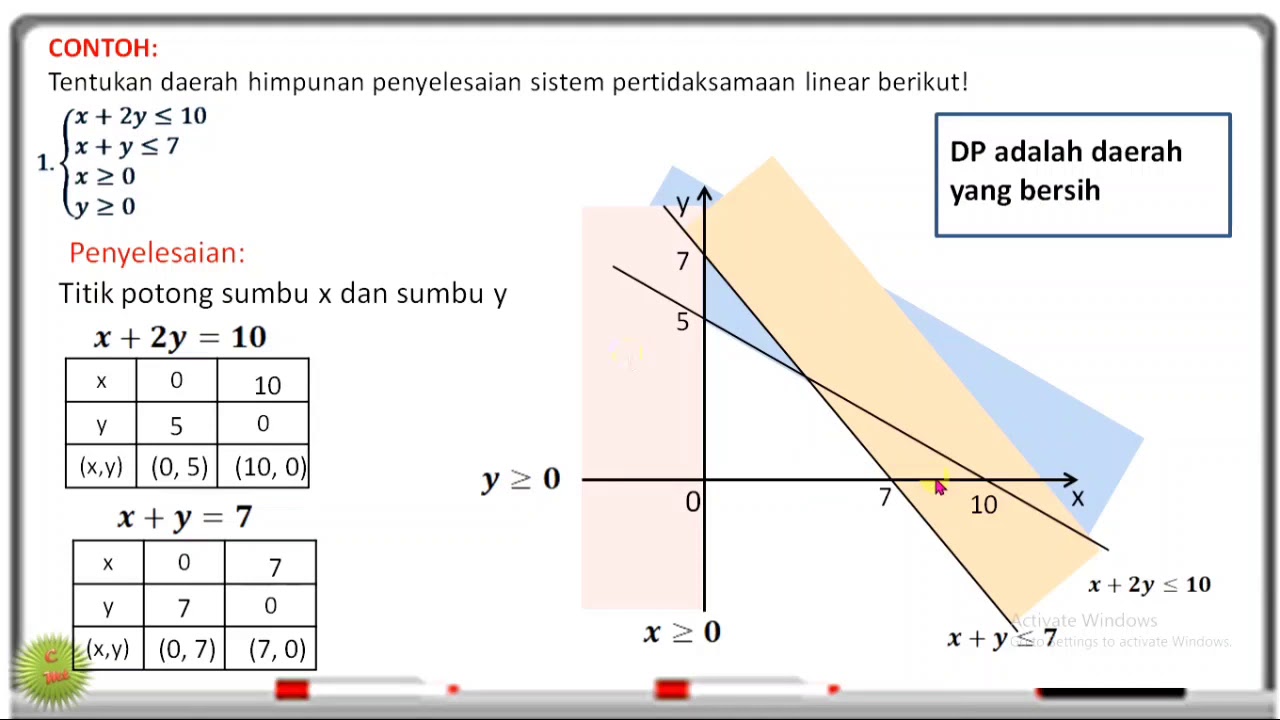
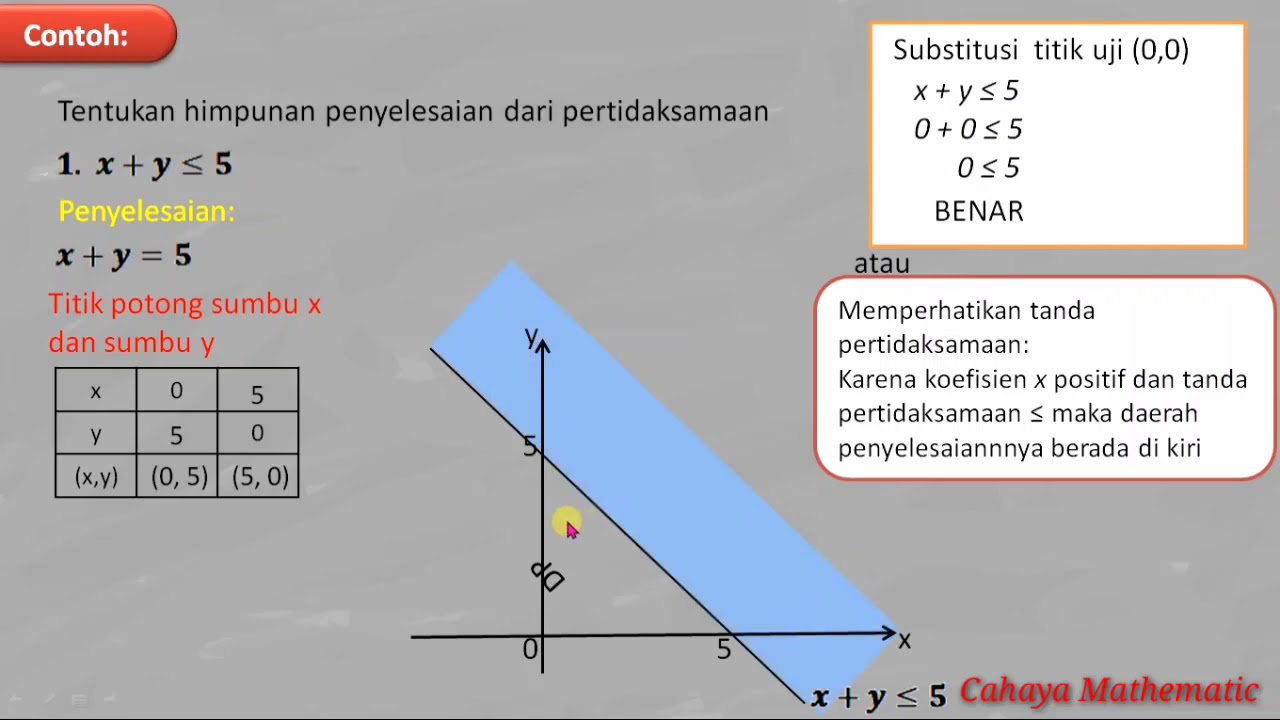
4 Steps to Solving Multi-Step Inequalities | 7.EE.B.4 💚
Summary
TLDRIn 'The Magic of Math' video, the host teaches how to solve multi-step inequalities using four key steps: clear parentheses, isolate the variable, get a coefficient of one, and graph the solution. The tutorial employs prior knowledge of equations to guide viewers through examples, emphasizing the importance of maintaining inequality properties throughout the process. The lesson aims to make mastering math approachable and engaging.
Takeaways
- 📘 The lesson focuses on solving multi-step inequalities, which requires understanding and applying prior knowledge of solving equations and inequalities.
- 🔍 There are four key steps to solving multi-step inequalities: clearing parentheses, isolating the variable term, simplifying the variable to a coefficient of one, and graphing the solution.
- 👉 Step one involves using the distributive property to clear parentheses if necessary.
- 🔄 Step two circles the variable term and adds or subtracts values from both sides to isolate the variable.
- 🔄 Step three circles the variable and involves multiplying or dividing by a value to simplify the variable's coefficient to one.
- 📊 Step four is graphing the solution on a number line, using appropriate symbols for the inequality type (e.g., open or closed circles).
- ⚠️ It's important to remember that operations in front of terms can indicate whether they are positive or negative, affecting the direction of the inequality.
- ➗ When dividing both sides of an inequality by a negative number, the inequality symbol must be reversed.
- 📐 The process includes creating 'zero pairs' to isolate the variable term, which involves performing the inverse operation to what is already present.
- 📈 The video provides examples of solving inequalities with different operations, emphasizing the need to maintain the properties of equality when manipulating both sides of an inequality.
- 📚 The lesson encourages viewers to practice solving inequalities by pausing the video and attempting the problems themselves, then checking their work against the provided solutions.
Q & A
What is the main topic of the 'Magic of Math' video?
-The main topic of the video is solving multi-step inequalities.
What are the four steps to solving multi-step inequalities as outlined in the video?
-The four steps are: 1) Clear parentheses by performing the distributive property if necessary, 2) Circle the variable term and add or subtract a value from both sides to isolate it, 3) Circle the variable and multiply or divide a value from both sides to get a coefficient of one, and 4) Graph the solution.
Why might steps one and two not be necessary when solving multi-step inequalities?
-Steps one and two might not be necessary if the inequality does not have parentheses that require clearing or if the variable term is already isolated.
What is the end goal when solving for the variable in an inequality?
-The end goal is to have the variable with a coefficient of one, so you can determine what the variable is less than, greater than, or equal to.
How does the video suggest handling negative values when solving inequalities?
-When multiplying or dividing by a negative value, you must reverse the inequality symbol to maintain the correct relationship.
What symbol should be used on a number line to represent a value that the variable can be equal to?
-A closed circle should be used on the number line to represent a value that the variable can be equal to.
What symbol should be used on a number line to represent a value that the variable cannot be equal to?
-An open circle should be used on the number line to represent a value that the variable cannot be equal to.
How does the video suggest identifying the variable term in an inequality?
-The video suggests identifying the variable term by looking at what operation is applied to it and noting whether it's positive or negative.
What is the purpose of creating a 'zero pair' when solving inequalities?
-Creating a 'zero pair' is done to isolate the variable term by eliminating the constant that is added or subtracted from it.
What should you do when you encounter parentheses in an inequality that requires solving?
-When encountering parentheses, you should perform the distributive property to clear them before proceeding with the other steps.
How does the video demonstrate the process of solving a multi-step inequality?
-The video demonstrates the process by walking through several examples, showing each step from isolating the variable to graphing the solution on a number line.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)