Introduction to Hypothesis Testing

Summary

In this video, Professor Dan Kernel introduces the concept of hypothesis testing using U.S. census data and a sample of children of immigrants. He demonstrates how to analyze sample proportions and explores the idea of statistical significance. The video covers key statistical concepts such as null and alternative hypotheses, type 1 and type 2 errors, and the process of hypothesis testing, including p-values and critical values. It emphasizes the importance of thoughtful interpretation in hypothesis testing while addressing common pitfalls like sample size effects, p-hacking, and publication bias in research.

Q & A

What is hypothesis testing, as introduced in the video?

Hypothesis testing is a statistical process used to determine if there is enough evidence in a sample of data to support a particular hypothesis about a population parameter. The process involves comparing sample data to what is expected under a null hypothesis.

What is the primary dataset used in the video to explain hypothesis testing?

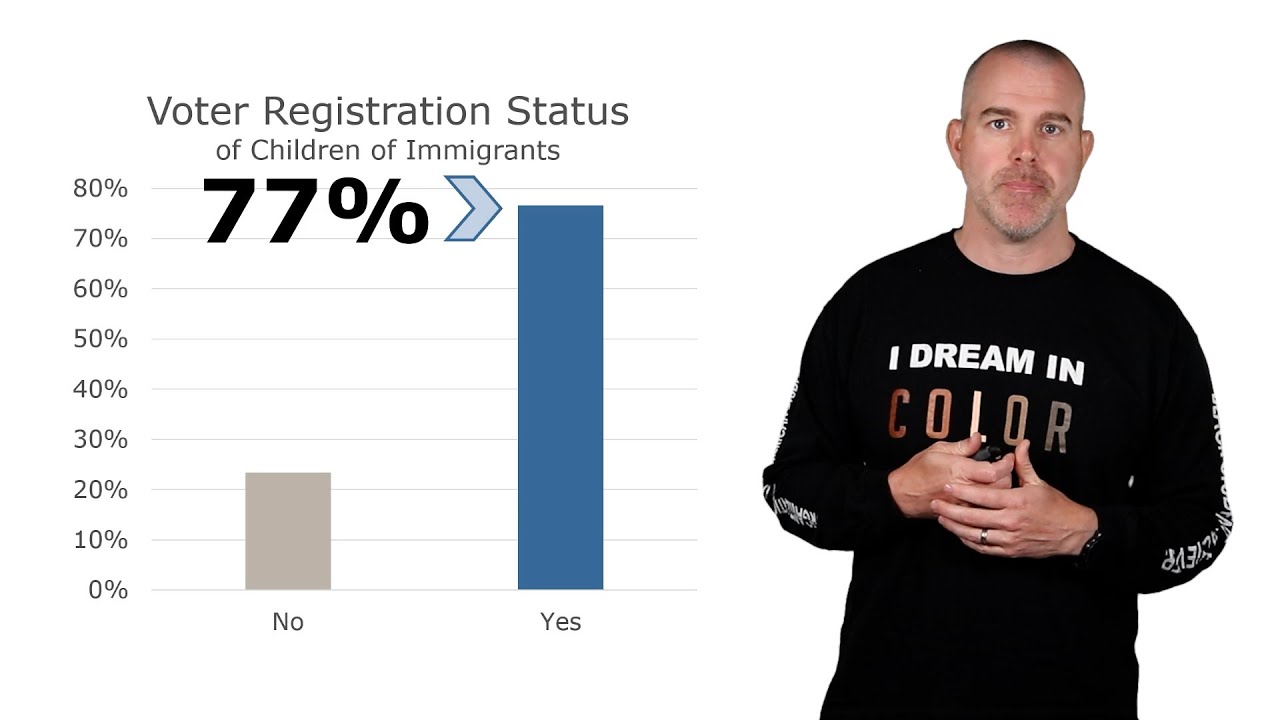
The primary dataset used in the video comes from U.S. Census data, which reports that 42.3% of the population aged 25 and older have at least an associate's degree. The video compares this data to a sample of children of immigrants, where 56.9% have an associate's degree or higher.

What is the null hypothesis in the video’s example?

The null hypothesis in the example is that the proportion of children of immigrants who have at least an associate's degree is the same as the population proportion, 42.3%.

What is the alternative hypothesis in the example provided?

The alternative hypothesis is that the proportion of children of immigrants who have at least an associate's degree is greater than the population proportion of 42.3%.

What is the importance of checking if sample proportions are normally distributed in hypothesis testing?

In hypothesis testing, checking if sample proportions are normally distributed ensures that the sampling distribution follows the normal curve, allowing for the application of standard statistical methods like z-tests. This is important for accurately calculating probabilities and making valid inferences.

What is the significance of the sample size in hypothesis testing?

Sample size plays a crucial role in hypothesis testing because a larger sample size leads to a smaller standard deviation of the sample proportions. This can make even small differences in proportions seem statistically significant, so sample size should be carefully considered.

What are Type 1 and Type 2 errors in hypothesis testing?

A Type 1 error occurs when the null hypothesis is rejected when it is actually true. A Type 2 error happens when the null hypothesis is not rejected when the alternative hypothesis is actually true.

How do the critical value and p-value methods differ in hypothesis testing?

The critical value method involves comparing the test statistic to a predefined critical value, and if the test statistic falls into the critical region, the null hypothesis is rejected. The p-value method calculates the probability of observing a sample statistic as extreme as the one obtained, and if the p-value is less than the significance level, the null hypothesis is rejected.

Why is the 0.05 significance level commonly used in hypothesis testing?

The 0.05 significance level is commonly used because it strikes a balance between making Type 1 and Type 2 errors. It represents a 5% chance of incorrectly rejecting the null hypothesis, which is generally considered acceptable in many fields of research.

What is a potential issue with p-values in hypothesis testing, as mentioned in the video?

A major issue with p-values is publication bias, where studies with significant p-values are more likely to be published. Additionally, p-hacking, or repeating experiments until a significant result is found, can lead to misleading conclusions. This highlights the need for careful interpretation of p-values.