Sistemas de ecuaciones lineales 2x2 | Determinantes - Método de Cramer | Ejemplo 1
Summary
TLDREn este video tutorial, se presenta el método de Cramer para resolver sistemas de ecuaciones lineales de 2x2, también conocido como el método de determinantes. El instructor explica cómo encontrar el determinante del sistema, y luego cómo calcular los determinantes cambiando cada variable para determinar sus valores respectivamente. Seguidamente, se resuelve un ejemplo práctico y se ofrece un ejercicio para que los estudiantes prueben sus habilidades. El video termina con una invitación a suscribirse y seguir el curso completo disponible en el canal.
Takeaways
- 😀 El video ofrece un curso sobre cómo resolver sistemas de ecuaciones lineales de 2x2 utilizando el método de determinantes de Kramer.
- 📚 Se explica que para resolver un sistema es necesario encontrar el valor de 'x' e 'y', y esto se hace a través de una división.
- 🔍 El método de determinantes, también conocido como método de Kramer, es considerado uno de los más sencillos para resolver sistemas de ecuaciones.
- 📝 Antes de calcular los determinantes, se debe asegurar que las ecuaciones estén bien ordenadas con las variables a la izquierda y los coeficientes independientes a la derecha.
- 📐 Se describe el proceso para encontrar el determinante del sistema, que es fundamental para el método de Kramer.
- 🧩 Se menciona que para encontrar el valor de 'x', se calcula el determinante cambiando 'x' y se divide entre el determinante del sistema.
- 🔄 Del mismo modo, para encontrar 'y', se calcula el determinante cambiando 'y' y se divide por el determinante del sistema.
- 📉 Se ilustra cómo calcular el determinante cambiando 'x', colocando los términos independientes en lugar de 'x' y manteniendo los coeficientes de 'y'.
- 📈 Se hace hincapié en la importancia de realizar los cálculos de multiplicación y resta para obtener el valor del determinante.
- 🔢 Se proporciona un ejemplo práctico para calcular el determinante del sistema y el determinante cambiando 'x', obteniendo el valor de 'x'.
- 🔄 Se repiten los pasos para encontrar el determinante cambiando 'y', para luego obtener el valor de 'y' y resolver así el sistema de ecuaciones.
Q & A
¿Qué es el método de Kramer y cómo se relaciona con los sistemas de ecuaciones lineales de 2x2?
-El método de Kramer, también conocido como el método de determinantes, es una técnica para resolver sistemas de ecuaciones lineales de 2x2. Se basa en el cálculo de dos determinantes: uno del sistema completo y otro donde se reemplaza una variable por el término independiente, para luego dividir ambos resultados y encontrar el valor de la variable en cuestión.
¿Cómo se verifica si un sistema de ecuaciones está ordenado antes de aplicar el método de Kramer?
-Para aplicar el método de Kramer, es necesario que el sistema esté ordenado, con las variables (x e y) a la izquierda de la igualdad y los coeficientes independientes a la derecha. Si no está ordenado, se debe reorganizar antes de proceder con el cálculo de los determinantes.
¿Cuál es el primer paso para encontrar el determinante del sistema en el método de Kramer?
-El primer paso es escribir los coeficientes de las variables (x e y) en el triángulo del determinante y los coeficientes independientes debajo, luego se realiza la operación de multiplicar los productos diagonales y restarlos entre sí para obtener el valor del determinante del sistema.
¿Cómo se calcula el determinante cambiando la x en el método de Kramer?
-Para calcular el determinante cambiando la x, se reemplaza el coeficiente de la x en el determinante original por los términos independientes de las ecuaciones, y se realiza el mismo proceso de multiplicación y resta para obtener el nuevo determinante.
¿Cómo se calcula el determinante cambiando la y en el método de Kramer?
-Similar al cálculo del determinante cambiando la x, pero en este caso se reemplaza el coeficiente de la y por los términos independientes, y se calcula el determinante siguiendo el proceso de multiplicación y resta.
¿Qué se hace con los determinantes calculados para encontrar el valor de x en el método de Kramer?
-Se divide el determinante cambiando la x entre el determinante del sistema completo, y el resultado da el valor de x en el sistema de ecuaciones.
¿Cómo se determina el valor de y utilizando el método de Kramer?
-Se divide el determinante cambiando la y entre el determinante del sistema completo, lo que proporciona el valor de y en el sistema de ecuaciones.
¿Qué ocurre si al dividir los determinantes no se obtiene un número entero en el método de Kramer?
-Si la división no resulta en un número entero, se simplifica el cociente hasta obtener una fracción o decimal, lo que indica que la solución no es un entero. Si no se puede dividir, es posible que no haya solución única o que el sistema no tenga solución.
¿Cómo se verifica la solución obtenida con el método de Kramer?
-Para verificar la solución, se reemplazan los valores encontrados en las variables x e y en las ecuaciones originales y se comprueba si ambas ecuaciones se balancean, es decir, si ambas son verdaderas.
¿Cuál es el propósito del ejercicio que se deja al final del script del video?
-El ejercicio al final del script es para que los espectadores practiquen los conceptos aprendidos y apliquen el método de Kramer para resolver un sistema de ecuaciones lineales de 2x2 por sí mismos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Sistemas de ecuaciones lineales 2x2 INTRODUCCIÓN

4 Métodos en 5 minutos para resolver sistema de ecuaciones lineales 2x2

Método de CRAMER para resolver SISTEMAS 📝 Sistemas de Ecuaciones
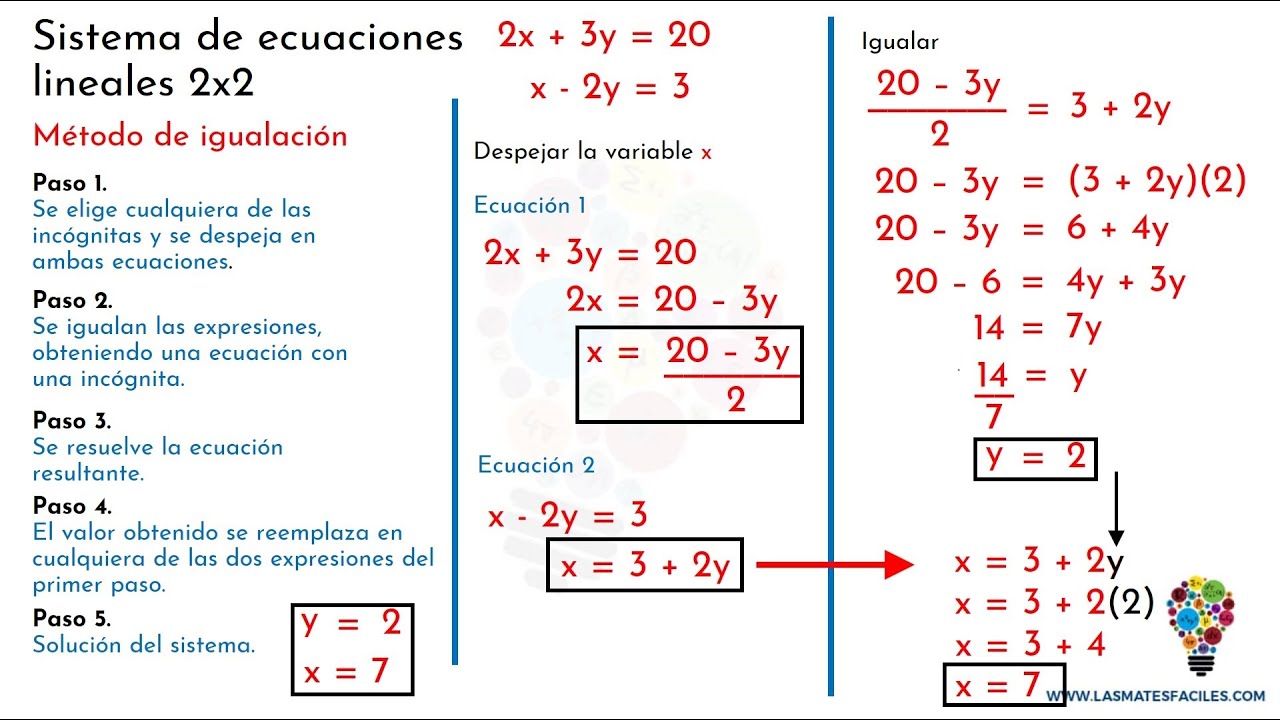
Sistemas de Ecuaciones 2x2 - Método de Igualación

Sistema de ecuaciones 2x2. Método de suma y resta.Álgebra

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción
5.0 / 5 (0 votes)
