Section 1 Worksheet Solutions: CSPs
Summary
TLDRThis video script discusses Constraint Satisfaction Problems (CSPs) using two examples: scheduling professors to classes and Pac-Man navigating corridors. It explains how to identify variables and values, formulate constraints, and apply techniques like forward checking and arc consistency. The script also covers the use of the Minimum Remaining Values (MRV) heuristic and proposes an efficient solution for CSPs structured as rings, using cut-set conditioning to transform the problem into a tree-like structure for easier solving.
Takeaways
- 📘 The topic of the handout is about formulating a Constraint Satisfaction Problem (CSP) for scheduling professors to teach classes.
- 🔄 In CSP formulation, classes are the variables and professors are the values, with the goal of assigning one professor to each class.
- 🚫 Unary constraints are used to represent qualifications of professors, limiting which classes they can teach.
- 🔄 Binary constraints are used to prevent the same professor from teaching overlapping classes.
- 📊 The domains for each class are determined after enforcing unary constraints, which reduce the pool of eligible professors for each class.
- 🔗 Binary constraints are identified by overlapping class times, creating a network of constraints between classes.
- 🌐 A constraint graph is constructed by connecting nodes (classes) with edges where constraints exist between them.
- 🎲 The Pac-Man problem is introduced as a CSP with variables as corridors and values as types of corridors (pit, ghost, or exit).
- 🌬 Breezes felt by Pac-Man between corridors lead to constraints about the types of corridors that must produce those breezes.
- 🚫 Adjacent corridors cannot both be exits, adding another constraint to the problem.
- 🔍 Forward checking in CSP involves testing the consistency of assignments and pruning values that do not satisfy constraints.
- 🔄 The process of maintaining CSP consistency includes enforcing unary constraints first and then checking binary constraints for consistency.
- 🔑 The Minimum Remaining Values (MRV) strategy is suggested for choosing the next variable to assign in the CSP.
- 📈 The script discusses the efficiency of solving CSPs in a ring structure by using cut-set conditioning to transform the problem into a tree-like structure.
- 🌳 The tree CSP algorithm is highlighted as a method to solve problems without backtracking by ensuring parent-to-child arc consistency.
- 🔙 Backtracking behavior in standard backtracking search with enforced consistency is explained, ensuring that the first variable chosen will lead to a solution.
Q & A
What is the main topic of the handout for discussion in the script?
-The main topic of the handout for discussion is on Constraint Satisfaction Problems (CSPs) with a focus on scheduling professors for classes and the trapped Pac-Man problem.
What are the two entities identified in the first problem of scheduling professors for classes?
-The two entities identified are the classes and the professors, where classes are the variables and professors are the values these variables can take.
What are the two main types of constraints mentioned in the script for the professor scheduling problem?
-The two main types of constraints are unary constraints, which involve one variable (e.g., a professor's qualifications for a class), and binary constraints, which involve two variables (e.g., overlapping class times preventing the same professor from teaching both).
How does the script represent the constraints for the Pac-Man problem?
-The script represents constraints for the Pac-Man problem by considering the breezes produced by different corridor types and the fact that neighboring corridors cannot both be exits.
What is the purpose of forward checking in CSPs as described in the script?
-The purpose of forward checking is to ensure that the arcs in the CSP are consistent by testing each value in the domain of one variable against the domain of the connected variable, pruning values that do not satisfy the constraints.
What does the script suggest as an efficient method for solving a CSP in the form of a ring, like the trapped Pac-Man problem?
-The script suggests using cut-set conditioning by fixing one variable to transform the ring into a tree structure, which can then be efficiently solved using tree CSP algorithms.
What is the Minimum Remaining Values (MRV) strategy mentioned in the script, and how does it help in solving CSPs?
-The MRV strategy involves choosing the variable with the smallest number of remaining values to assign next, which helps in reducing the search space and potentially finding a solution more quickly.
How does the script describe the process of enforcing unary constraints in the Pac-Man problem?
-The script describes enforcing unary constraints by removing certain values from the domains of specific variables based on the constraints (e.g., removing 'pit' from the domains of corridors that cannot be pits).
What is the significance of the constraint graph in the script, and how is it constructed?
-The constraint graph is significant as it visually represents the constraints between variables in a CSP. It is constructed by drawing nodes for each variable and edges between nodes that share constraints.
How does the script explain the process of consistency enforcement in the CSP for the Pac-Man problem?
-The script explains consistency enforcement by putting every arc in the CSP into a queue and processing them one by one to ensure they are consistent. This involves checking if values in the domain of one variable can be assigned without violating constraints with the connected variable.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Constraint Satisfaction Problems (CSPs) 1 - Overview | Stanford CS221: AI (Autumn 2021)

Constraint Satisfaction: the AC-3 algorithm
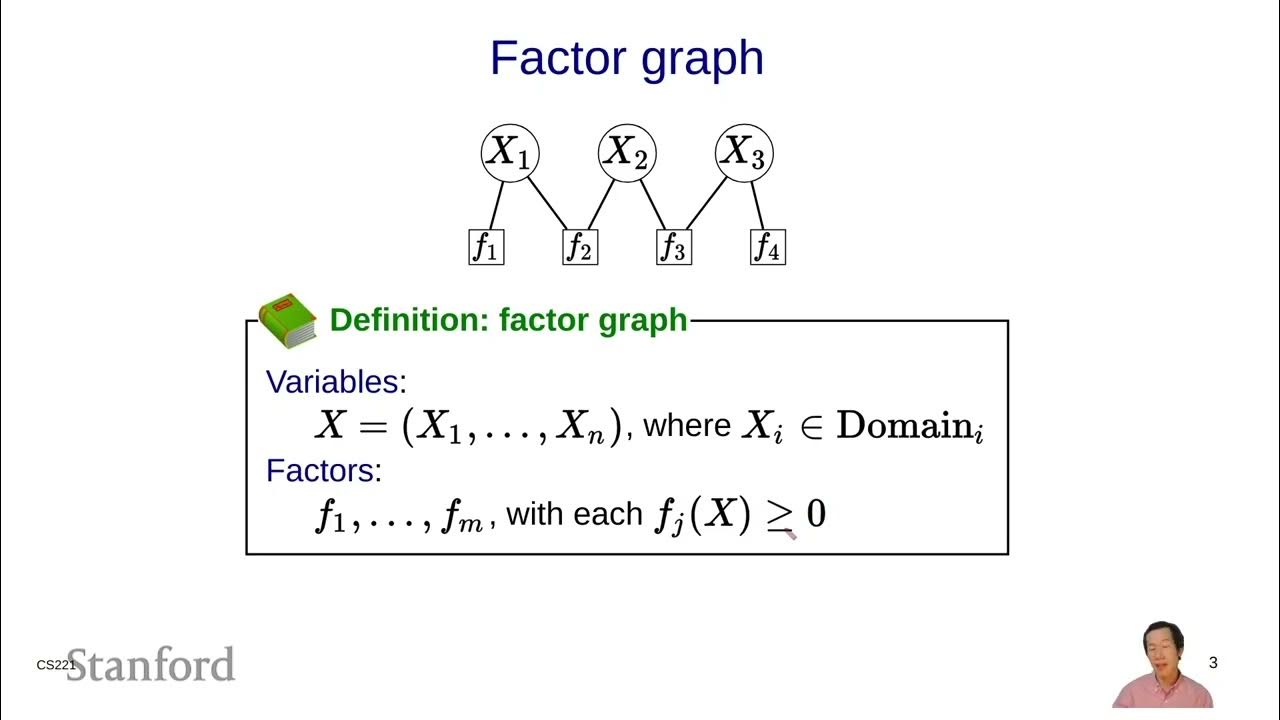
Constraint Satisfaction Problems (CSPs) 2 - Definitions | Stanford CS221: AI (Autumn 2021)

An Introduction To Constraint Programming - Jacob Allen

Pewarnaan Graf (Graph Coloring) PART 1 | Algoritma Welch Powell & Contoh kasus penjadwalan kuliah

CS3491 AIML – Constraint Satisfaction Problem (CSP) with Example in tamil
5.0 / 5 (0 votes)