Applying First Principles to x² (1 of 2: Finding the Derivative)
Summary
TLDRThe video script explains the concept of a derivative in calculus, focusing on how the gradient of a curve changes and cannot be represented by a single constant. It introduces the gradient as a function, leading to the concept of the derivative, which is a function itself. The script discusses the process of finding the derivative from first principles using the limit of the difference quotient. The explanation emphasizes understanding the concept rather than rote memorization and applies it to a specific example involving the function f(x) = x².
Takeaways
- 📚 The concept of 'rise over run' is revisited in the context of a curve where the gradient is not constant but changes, leading to the idea of a gradient function.
- 🔍 The term 'derivative' is introduced as the rate of change of a function, symbolized as f'(x) or \( \frac{dy}{dx} \), which represents the gradient function.
- 📈 The process of finding the derivative involves taking the limit of the rise over run as the run approaches zero, which is the definition of the derivative.
- 👉 The notation f'(x) is used when the function is named 'f', while \( \frac{dy}{dx} \) is used in more general contexts without a specific function name.
- 🚫 Memorizing the process without understanding is discouraged; the importance of grasping the underlying concepts is emphasized.
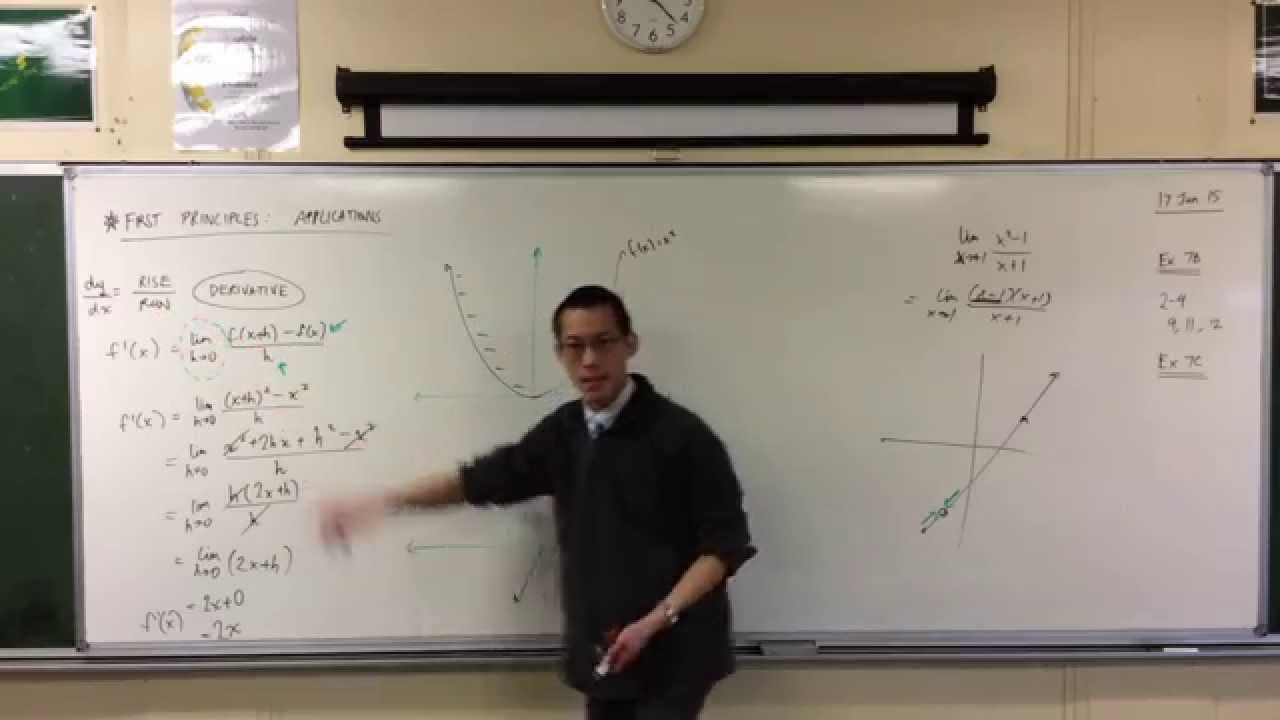
- 🔑 The derivative is calculated by finding the limit as \( h \) approaches zero in the expression \( \frac{f(x+h) - f(x)}{h} \).
- 📉 The example of the parabola f(x) = x^2 is used to demonstrate the process of finding the derivative from first principles.
- 🔄 The process involves algebraic manipulation to simplify the expression and isolate the variable \( h \) to cancel it out before taking the limit.
- 🚫 The limit cannot be taken at \( h = 0 \) directly due to division by zero, but the behavior as \( h \) approaches zero is considered.
- 📌 The derivative of f(x) = x^2 is found to be 2x, which represents the slope of the tangent line to the curve at any point.
- 🔍 The concept of a 'hole' in the derivative function at x = -1 is discussed, indicating a point where the derivative does not exist.
Q & A
What is the concept of 'rise over run' in the context of a curve with changing gradient?
-In the context of a curve with a changing gradient, 'rise over run' is not a constant but a function itself. It represents the change in y (rise) over the change in x (run), and is expressed as dy/dx, which is the gradient function of the curve.
Why can't we use the term 'gradient' in the traditional sense for a curve with a variable slope?
-We can't use the term 'gradient' in the traditional sense because for a curve with a variable slope, the gradient is not a constant value; it changes at every point on the curve, hence it is better described as a gradient function.
What is the term used to describe the gradient of a function?
-The term used to describe the gradient of a function is 'derivative'. It signifies that the gradient is derived from the original function and is itself a function.
How is the derivative of a function represented mathematically?
-The derivative of a function is represented mathematically as f'(x), which is another way of indicating the notation for the gradient function of f(x).
What is the significance of the limit as h approaches zero in the context of derivatives?
-The limit as h approaches zero is used to find the derivative of a function at a specific point. It helps in transitioning from the concept of the gradient between two points (secant) to the gradient at a single point (tangent).
Why is it important to understand the origin of mathematical concepts like derivatives?
-Understanding the origin of mathematical concepts like derivatives is crucial for true comprehension. It prevents mere memorization without grasping the underlying principles, which is essential for applying these concepts effectively.
What is the difference between the gradient of a tangent and the gradient of a secant?
-The gradient of a tangent is the instantaneous rate of change at a specific point on a curve, while the gradient of a secant is the average rate of change between two points on the curve. The limit as h approaches zero is used to find the tangent's gradient, which is the derivative.
What is the process of finding the derivative of a function from first principles?
-The process involves taking the limit of the difference quotient (f(x+h) - f(x)) / h as h approaches zero. This manipulation helps in isolating h and finding the derivative at a particular point on the function.
Can you provide an example of finding the derivative of a simple function, like f(x) = x^2?
-Yes, for f(x) = x^2, the derivative f'(x) is found by taking the limit as h approaches zero of (x+h)^2 - x^2 / h, which simplifies to 2x after canceling out terms and applying the limit.
Why is there a hole in the graph of the function (x^2 - x^2) / h as h approaches zero?
-There is a hole at x = -1 because when h approaches zero, the expression (x+h)^2 - x^2 simplifies to 2x + h, and when x = -1, the term 2x + h becomes zero, leading to division by zero, which is undefined.
How does the concept of limits help in understanding the behavior of a function at a point where direct calculation is not possible?
-The concept of limits allows us to understand the behavior of a function as it approaches a certain point, even when direct calculation is not possible due to division by zero or other undefined operations. It provides a meaningful result by showing the trend or value the function is approaching.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

12.2 Finding the derivative (PURE 1- Chapter 12: Differentiation)
Applying First Principles to x² (2 of 2: What do we discover?)

Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy

Übersicht f f´ f´´, Zusammenhänge der Funktionen/Graphen, Ableitungsgraphen | Mathe by Daniel Jung

12.1 Gradients of curves (PURE 1- Chapter 12: Differentiation)

A-level Mathematics Pure 1 Chapter 9 Integration
5.0 / 5 (0 votes)
