Translasi Titik

Summary

In this video, the instructor introduces the concept of transformation in mathematics, specifically focusing on the topic of translation. He explains how transformation refers to changes in the position or size of an object, using the analogy of the 'Transformer' movie. The instructor covers four main types of transformations: translation, reflection, rotation, and dilation. This video specifically focuses on translation, explaining how a point’s position shifts on a coordinate plane using steps to move horizontally and vertically. Examples are provided, demonstrating how to calculate the new coordinates after applying translation vectors.

Takeaways

• 😀 Transformasi (transformation) in mathematics refers to changes in the position and/or size of an object, particularly in the context of geometric transformations like translation, reflection, rotation, and dilation.
• 😀 The term 'transformasi' shares its roots with the word 'transformer,' which refers to things that change form (e.g., vehicles transforming into robots in the movie 'Transformers').
• 😀 In high school mathematics, transformations are discussed as changes in the location (position) or size of a point on the coordinate plane.
• 😀 One common transformation is 'translasi' (translation), which involves shifting a point's position in either horizontal (x-axis) or vertical (y-axis) direction, or both.
• 😀 To translate a point, you shift it by a certain number of units along the x-axis (right/left) and y-axis (up/down). For example, moving a point 2 steps to the right and 3 steps up.
• 😀 After translating a point, the new position is typically expressed with coordinates written in the form of the original point's letter followed by an accent (e.g., A' for the translated point).
• 😀 Translating a point on the coordinate plane can be visualized by counting steps in the horizontal and vertical directions from the original point.
• 😀 Translation can be represented as a vector, where the vector indicates the number of steps in the x-direction (horizontal) and y-direction (vertical).
• 😀 Vectors for translation are written in the form (x, y), where positive values indicate movement right and up, while negative values indicate movement left and down.
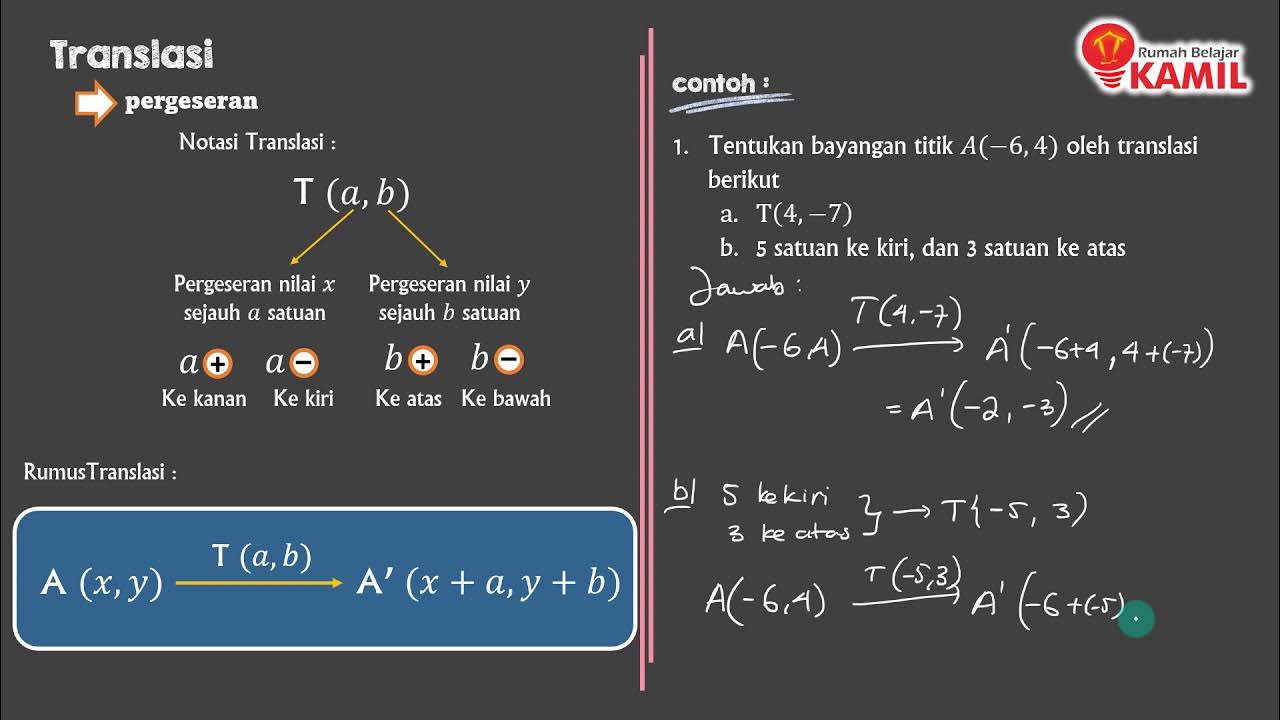
• 😀 To find the new coordinates after translation, simply add the translation vector to the original point’s coordinates (e.g., for point A (3, 2) translated by vector (2, 3), the new coordinates would be (5, 5)).

Q & A

What is the main theme of the lesson in the transcript?

The main theme of the lesson is 'transformasi' (transformation) in mathematics, with a focus on the concept of translation (pergeseran or translasi). The lesson explains how transformations change the position or size of an object, with a particular emphasis on translation in coordinate geometry.

How is the term 'transformasi' connected to the concept of 'Transformers'?

The term 'transformasi' (transformation) is connected to the concept of 'Transformers' in that both refer to change or transformation. In the movie 'Transformers', various objects, like trucks or animals, change or 'transform' into robots, which mirrors the mathematical concept of transformation, where objects change their position or size.

What is meant by 'translation' or 'pergeseran' in mathematics?

In mathematics, 'translation' (or 'pergeseran') refers to the movement of a point from its original position to a new position, without changing its orientation or size. This can occur in a horizontal direction (left or right), vertical direction (up or down), or both.

How does the example with point A explain the concept of translation?

In the example with point A, the point is shifted two steps to the right and three steps upwards. After translation, the new coordinates of point A are (5, 5). This demonstrates how translation changes the position of a point on the coordinate plane.

What is the significance of the vector in translation?

The vector in translation represents the direction and distance by which a point is moved. It is written as an ordered pair of numbers, where the first number indicates horizontal movement (right or left), and the second number indicates vertical movement (up or down).

How can the coordinates of a point after translation be calculated using a vector?

To calculate the coordinates of a point after translation, you simply add the components of the translation vector to the original coordinates of the point. For example, if a point has coordinates (3, 2) and is translated by the vector (2, 3), the new coordinates are (3+2, 2+3) = (5, 5).

What happens when a point is translated using a vector with negative values?

When a point is translated using a vector with negative values, the point moves in the opposite direction. For example, a vector (-2, -3) means the point moves 2 steps to the left and 3 steps down.

Can you give an example of translating a point with negative coordinates?

Yes, if point C has coordinates (-2, 3) and is translated using the vector (-2, -3), we first move 2 steps to the left and 3 steps down. The new coordinates of point C after translation will be (-4, 0).

How can we simplify the process of finding the coordinates after translation?

The process can be simplified by directly adding the components of the translation vector to the original coordinates. For example, if the original point is (x, y) and the vector is (a, b), the new coordinates after translation will be (x + a, y + b).

Why does the teacher use the example of 'Transformers' to explain the concept of transformation?

The teacher uses the example of 'Transformers' because it provides a familiar and engaging analogy for students. In the movie, objects transform into robots, which helps students relate to the mathematical idea of transformation—changing positions or forms in a way that is tangible and easy to visualize.