Transform Calculus and its applications in Differential Equations
Summary
TLDRThis course introduces transform calculus and its application to differential equations. It explores the concept of transforming complex problems from one domain to another to simplify their solution. Key techniques covered include the Laplace transform for solving ordinary differential equations, as well as Fourier series and Fourier transforms for partial differential equations. The course demonstrates how these techniques can be applied in various engineering fields, making them valuable for students in disciplines like electrical, mechanical, and aerospace engineering, as well as for those in mathematics and physics. The goal is to equip students with powerful mathematical tools to solve engineering problems.
Takeaways
- 😀 Transform calculus is a technique that helps solve problems by transforming them from one domain to another, making them easier to solve.
- 😀 The main focus of this course is to teach the application of transform techniques in solving differential equations.
- 😀 Transform techniques like the Laplace and Fourier transforms help convert difficult differential equations into simpler algebraic or polynomial equations.
- 😀 The Laplace transform is a key technique for solving ordinary differential equations (ODEs) by converting them into algebraic equations.
- 😀 Fourier series and Fourier transforms are covered to help in solving partial differential equations (PDEs) by simplifying complex equations.
- 😀 The Fourier transform is used to simplify PDEs like parabolic, elliptic, and hyperbolic types, making them easier to solve.
- 😀 The course will explore the properties and theorems related to the Laplace and Fourier transforms and their applications in solving engineering problems.
- 😀 The primary goal is to teach analytical techniques to solve differential equations, offering an alternative to numerical methods that provide approximate solutions.
- 😀 Transform techniques are essential in various engineering fields such as electrical, mechanical, electronics, and aerospace, offering real-life problem-solving tools.
- 😀 This course is beneficial for students in engineering disciplines as well as for those studying mathematics or physics, providing them with valuable tools to solve complex problems.
Q & A
What is transform calculus?
-Transform calculus is a technique that allows us to transform a problem from one domain to another, making it easier to solve. Once solved in the new domain, the solution can be transformed back to the original domain.
Why is transform calculus useful in solving problems?
-Transform calculus helps in transforming complex problems, especially differential equations, into simpler algebraic or polynomial equations. This makes it easier to find solutions that are otherwise difficult to obtain in their original form.
What types of transformations are studied in this course?
-In this course, we focus on the Laplace transform, Fourier series, and Fourier transform. These transformations are used to simplify problems and find solutions more efficiently.
What is the Laplace transform and why is it important?
-The Laplace transform is a mathematical technique that transforms a differential equation into an algebraic equation, which is easier to solve. It is particularly useful for solving ordinary differential equations.
How does the Laplace transform simplify differential equations?
-The Laplace transform converts a differential equation into a simpler algebraic or polynomial equation, making it easier to solve. This avoids the complexities of directly solving the original differential equation.
What role does the Fourier series play in this course?
-The Fourier series helps in understanding the Fourier transform. It allows us to break down complex periodic functions into simpler sine and cosine components, which is essential for solving partial differential equations.
How are Fourier transforms used in solving partial differential equations?
-Fourier transforms are used to simplify partial differential equations, including parabolic, elliptic, and hyperbolic equations. These transforms convert the equations into simpler forms that are easier to solve analytically.
What are the real-life applications of these transform techniques?
-Transform techniques, such as Laplace and Fourier transforms, are widely used in engineering fields like electrical, mechanical, electronics, and aerospace. They help solve complex problems in these disciplines more efficiently.
Why are analytical solutions preferred over numerical solutions?
-Analytical solutions provide exact results, while numerical solutions only offer approximations. Transform techniques aim to obtain these exact solutions, which are often more reliable and precise.
Who will benefit from this course on transform techniques?
-Students studying engineering, as well as those pursuing undergraduate or postgraduate degrees in mathematics or physics, will find this course particularly valuable. It equips them with powerful tools to solve various complex problems in their respective fields.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Equações Diferenciais: Pra que Serve a Transformada de Laplace?
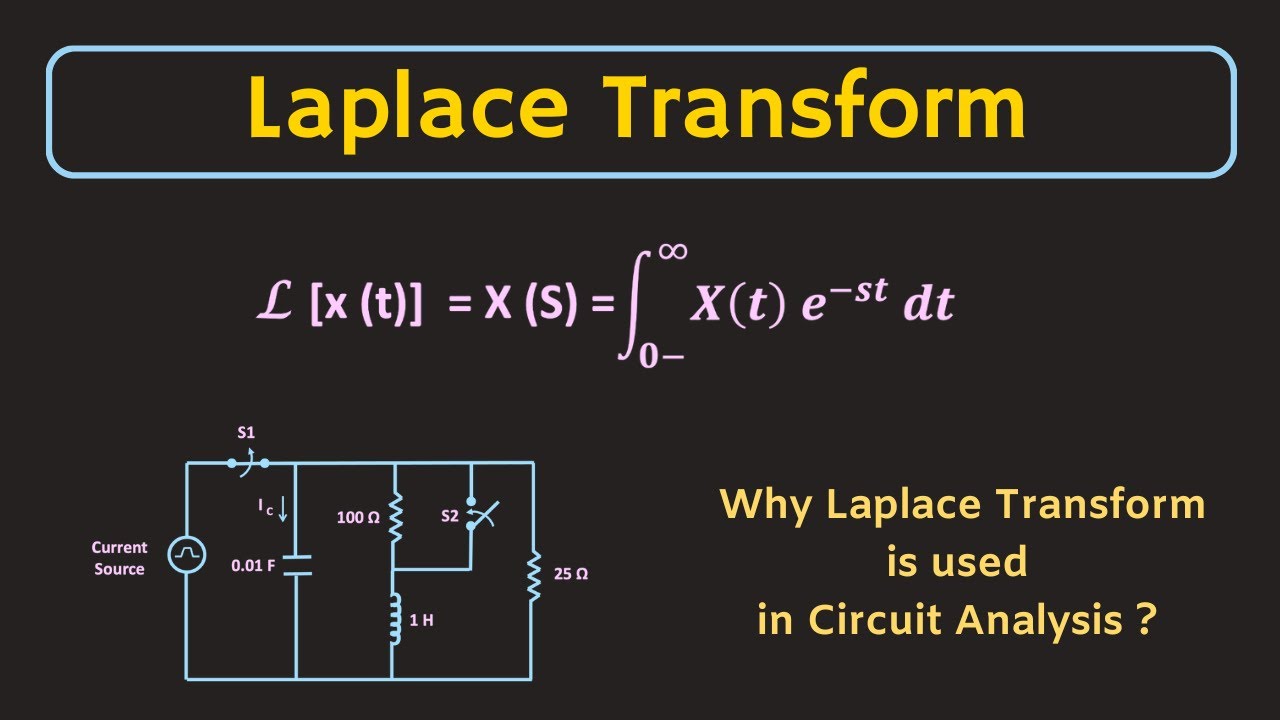
What is Laplace Transform? Why Laplace Transform is used in Circuit Analysis?

Review of Laplace Transform (Part 1)

The Physics of Euler's Formula | Laplace Transform Prelude

Lesson 1 - Laplace Transform Definition (Engineering Math)

Matching Slope Fields with Differential Equations
5.0 / 5 (0 votes)
