Introducción a la Programación Lineal
Summary
TLDREl script ofrece una introducción a la programación lineal, una técnica de la investigación de operaciones que busca maximizar o minimizar una función lineal bajo condiciones establecidas. Se discuten elementos clave como variables de decisión, funciones objetivo (maximización o minimización), restricciones y la condición de no negatividad. La importancia de identificar correctamente estas variables y restricciones para formular adecuadamente un modelo matemático se enfatiza, con el objetivo de encontrar soluciones óptimas a problemas cotidianos.
Takeaways
- 📚 La programación lineal es una rama de la investigación de operaciones que busca maximizar o minimizar una función lineal bajo ciertas condiciones.
- 📈 La función lineal se representa por una recta en el plano cartesiano y no incluye términos cuadráticos, cúbicos, trigonométricos, logarítmicos ni exponenciales.
- 🔍 Para resolver un problema de programación lineal, se debe convertir el problema en un modelo matemático utilizando variables, relaciones y funciones matemáticas.
- 🎯 Los modelos matemáticos de programación lineal están compuestos por variables de decisión, una función objetivo y restricciones.
- 🔑 Las variables de decisión son incógnitas que representan cantidades y son fundamentales para encontrar la solución al problema.
- 📊 Existen dos tipos de funciones objetivo: maximización (max) y minimización (min), dependiendo de si se busca obtener más ingresos o reducir costos.
- 🚧 Las restricciones son límites del sistema que se representan mediante ecuaciones y son esenciales para que la solución sea factible y realista.
- 📉 En problemas de maximización, se necesita al menos un límite superior, mientras que en problemas de minimización, se necesita al menos un límite inferior para la solución.
- 🚫 La condición de no negatividad impone que todas las variables de decisión deben ser mayores o iguales a cero, evitando valores negativos.
- 🤔 Para identificar variables de decisión y restricciones, es útil preguntarse qué se quiere conocer y cuáles son los recursos o requisitos limitados.
- 👋 El video ofrece una introducción teórica y promete un ejemplo práctico en el próximo video para ilustrar los conceptos aprendidos.
Q & A
¿Qué es la programación lineal?
-La programación lineal es una rama de la investigación de operaciones que busca maximizar o minimizar una función lineal, manteniéndose dentro de ciertas condiciones establecidas.
¿Por qué la programación lineal solo utiliza funciones lineales y no otras tipos de funciones?
-La programación lineal solo utiliza funciones lineales porque estas se pueden representar por rectas en el plano cartesiano, lo que permite encontrar soluciones óptimas de manera eficiente.
¿Cuáles son los componentes principales de un modelo de programación lineal?
-Los componentes principales de un modelo de programación lineal son las variables de decisión, la función objetivo y las restricciones.
¿Qué son las variables de decisión en la programación lineal?
-Las variables de decisión son las incógnitas que se desean conocer en el modelo matemático, generalmente representan cantidades como el número de unidades a producir o los kilos de un ingrediente en una mezcla.
¿Cómo se identifican las variables de decisión en un problema de programación lineal?
-Para identificar las variables de decisión, se hace la pregunta '¿Qué es lo que nos está pidiendo conocer el problema?', y las respuestas a esta pregunta guían en la elección correcta de las variables.
¿Cuáles son los dos tipos principales de funciones objetivo en la programación lineal?
-Los dos tipos principales de funciones objetivo son la maximización, representada con 'max', y la minimización, representada con 'min'.
¿Cuándo se utiliza la maximización en una función objetivo de programación lineal?
-Se utiliza la maximización cuando la función objetivo está relacionada con ingresos, utilidades o beneficios, ya que se busca obtener el mayor beneficio posible.
¿Qué representan las restricciones en un modelo de programación lineal?
-Las restricciones representan los límites del sistema, como tiempo, presupuesto o personal limitado, y son cruciales para que las soluciones sean factibles y realistas.
¿Cómo se identifican las restricciones en un problema de programación lineal?
-Para identificar las restricciones, se hace la pregunta '¿Qué recursos tengo limitados? ¿Tengo algún requisito que debo cumplir?', y las respuestas ayudan a plantear correctamente las restricciones.
¿Qué es la condición de no negatividad en un modelo de programación lineal y por qué es importante?
-La condición de no negatividad indica que todas las variables de decisión deben ser mayores o iguales a cero, lo que evita que las soluciones tomen valores negativos que no tienen sentido en la mayoría de los problemas.
¿Qué se debe tener en cuenta para convertir un problema cotidiano en un modelo matemático para la programación lineal?
-Se debe convertir el problema en números, relaciones, funciones o signos matemáticos, para poder hallar una solución al problema de programación lineal.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Método Simplex (2) Ejemplo Maximizar

Introducción a la Investigación de Operaciones
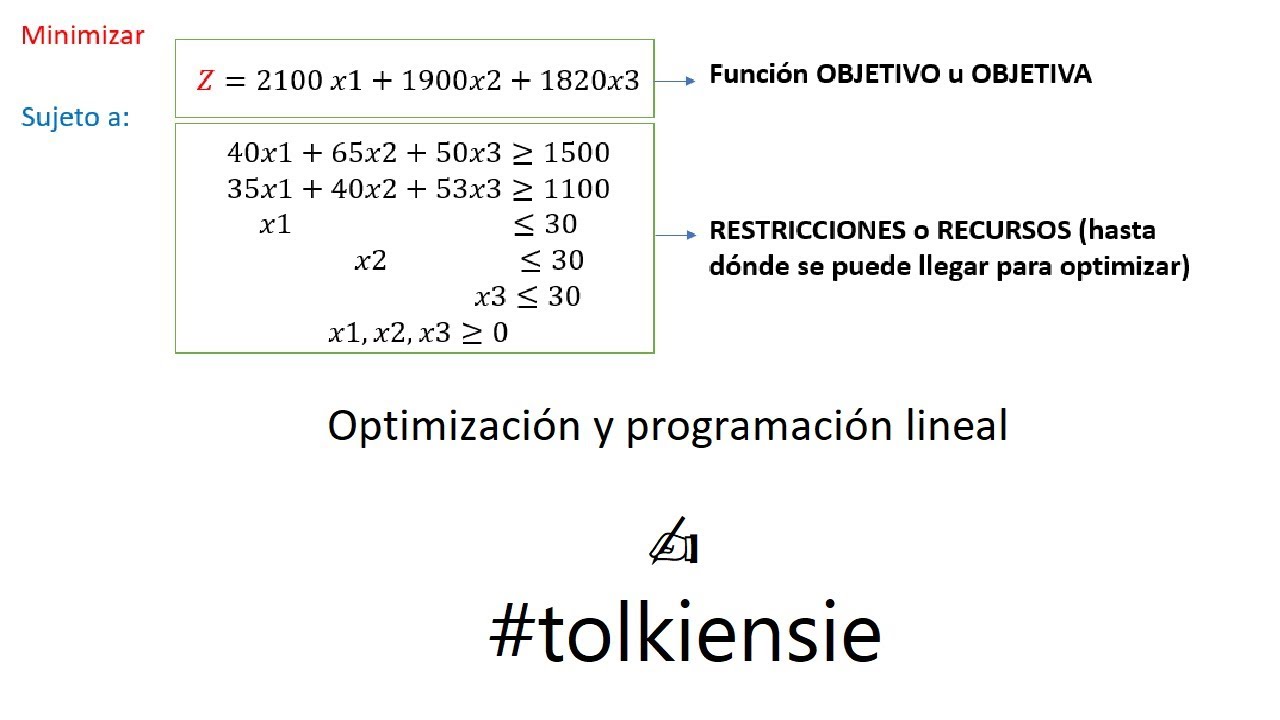
🔴PROGRAMACIÓN LINEAL partes restricciones solución método gráfico 2024 Optimización Max minimizar

Operations Research 03D: Linear Programming Graphical Solution Technique
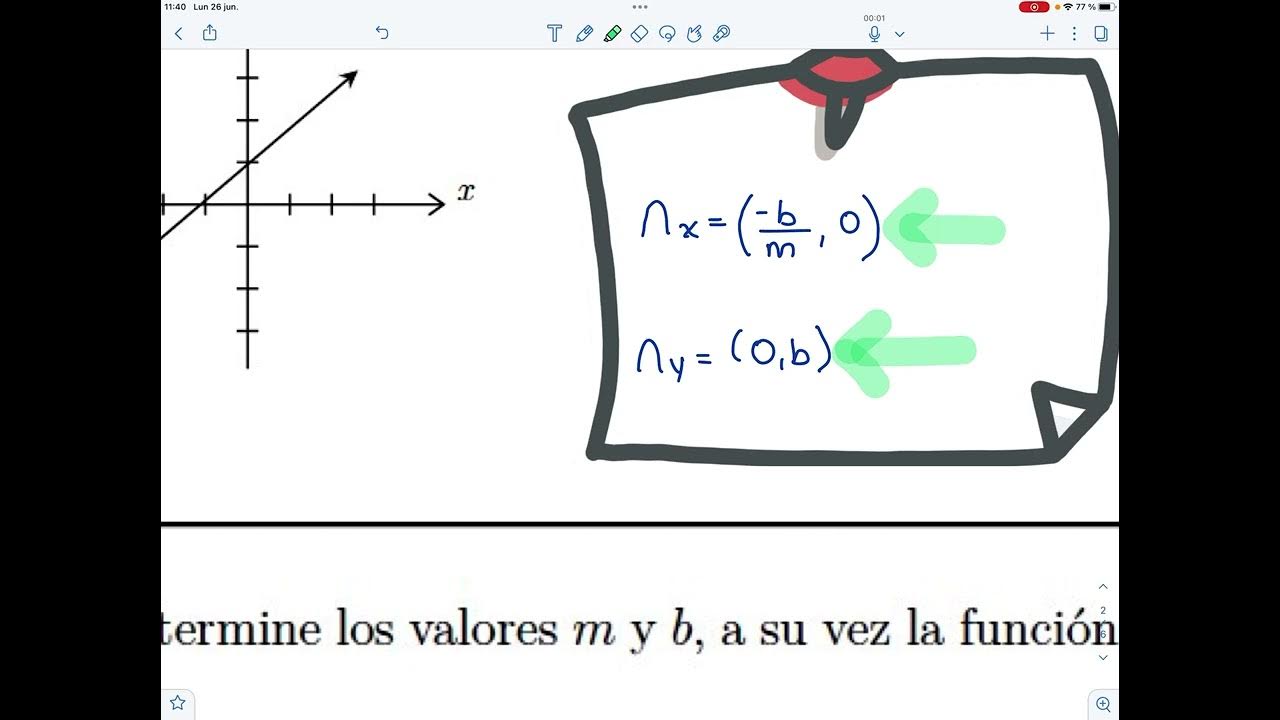
1 Funcion lineal

Análisis de Sensibilidad de la Función Objetivo
5.0 / 5 (0 votes)
