Ensaio triâxial (exercício 1)
Summary
TLDRThis video explains the steps of a triaxial test to calculate resistance parameters, normal, and tangential stresses during failure. The process involves determining effective and deviatoric stresses, applying the Mohr-Coulomb failure criterion, and analyzing the rupture point using geometry. Key concepts such as plotting the Mohr's circle, identifying rupture planes, and calculating normal and shear stresses are covered. The exercise includes the use of a 60-degree rupture angle and offers practical insights into how triaxial tests are conducted to understand soil behavior under stress.
Takeaways
- 😀 A triaxial test is being analyzed, focusing on effective stress and deviatoric stress during the failure point.
- 😀 The rupture point has an effective stress of 200 and a deviatoric stress of 800.
- 😀 The failure plane forms an angle of 60 degrees with the horizontal plane.
- 😀 The objective is to calculate the resistance parameters, normal stress, and tangential stress at the rupture point.
- 😀 The first step involves calculating the total stress by adding the effective stress and the deviatoric stress.
- 😀 The Mohr circle is drawn to represent the stresses, with the center located at 600.
- 😀 The rupture plane is located at 60 degrees from the horizontal, forming an important reference for the rupture point.
- 😀 The normal stress at the rupture point is calculated to be 400, and the tangential stress is 340.
- 😀 The theory of Mohr-Coulomb is applied to the problem, where the rupture plane intersects the Mohr circle.
- 😀 A perpendicular line from the center of the Mohr circle to the rupture plane is drawn, allowing the calculation of additional angles and stresses.
- 😀 The rupture angle is found to be 30 degrees, leading to a clear solution using geometry and Mohr's circle principles.
Q & A
What is the main goal of the triaxial test described in the script?
-The main goal of the triaxial test described is to determine the rupture stress parameters, including the effective stress and shear stress, and to calculate the normal and tangential stress at the point of rupture.
How are the rupture stresses calculated in the triaxial test?
-The rupture stresses are calculated by using the given tension values for effective stress (200 kPa) and deviatoric stress (800 kPa). The total stress is then obtained by adding these values, resulting in a stress circle. The normal and tangential stresses at the rupture point are determined using Mohr's Circle.
What role does Mohr's Circle play in solving the triaxial test problem?
-Mohr's Circle is used to visualize and calculate the normal and tangential stresses at the point of rupture. By plotting the effective stress and deviatoric stress on the circle, we can determine the rupture point, which helps in calculating the shear and normal stresses.
How is the rupture plane identified in the triaxial test?
-The rupture plane is identified by its angle of 60 degrees with respect to the horizontal. A horizontal plane is drawn, and the rupture plane is traced at a 60-degree angle, which intersects the stress circle at the rupture point.
What is the significance of the angle of 60 degrees in the triaxial test?
-The angle of 60 degrees represents the orientation of the rupture plane in relation to the horizontal. This is a key piece of information used to determine the point of rupture and is critical for calculating the corresponding stress values.
How are the normal and tangential stresses at the rupture point determined?
-The normal and tangential stresses at the rupture point are found by calculating the intercept of the rupture plane with the stress circle. The normal stress is 400 kPa, and the tangential (shear) stress is 340 kPa.
What is the role of the Mohr-Coulomb failure criterion in the analysis?
-The Mohr-Coulomb failure criterion is applied to describe the failure envelope, which is used to predict the rupture conditions. The analysis involves calculating the failure plane's angle and using this criterion to determine the shear strength of the material.
What does the perpendicular line to the Mohr's Circle represent?
-The perpendicular line from the center of the Mohr's Circle to the rupture plane represents the shear strength at the rupture point. This line helps in determining the stresses that cause failure in the material.
How is the angle of rupture (detrito angle) calculated?
-The angle of rupture, or detrito angle, is calculated using the geometry of the Mohr's Circle and the rupture plane. In this case, the detrito angle is determined to be 30 degrees.
What does the final solution tell us about the material's behavior under stress?
-The final solution reveals the material's response under the applied stresses, including the normal and tangential stresses at the point of rupture. It also provides the detrito angle and confirms the material's behavior according to the Mohr-Coulomb failure criterion.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
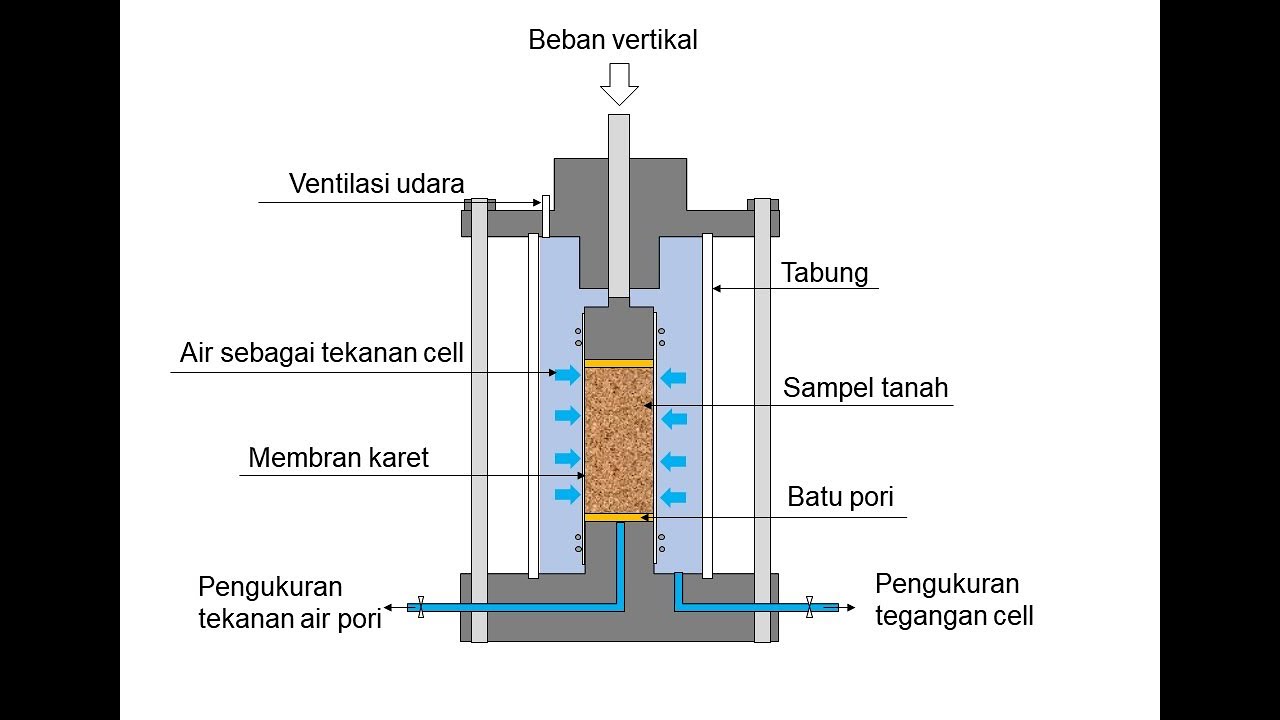
Triaxial

Triaxial Shear Test | Elementary Engineering

Chapter 12 Extra Example 1 - Direct shear test and Mohr's circle at failure
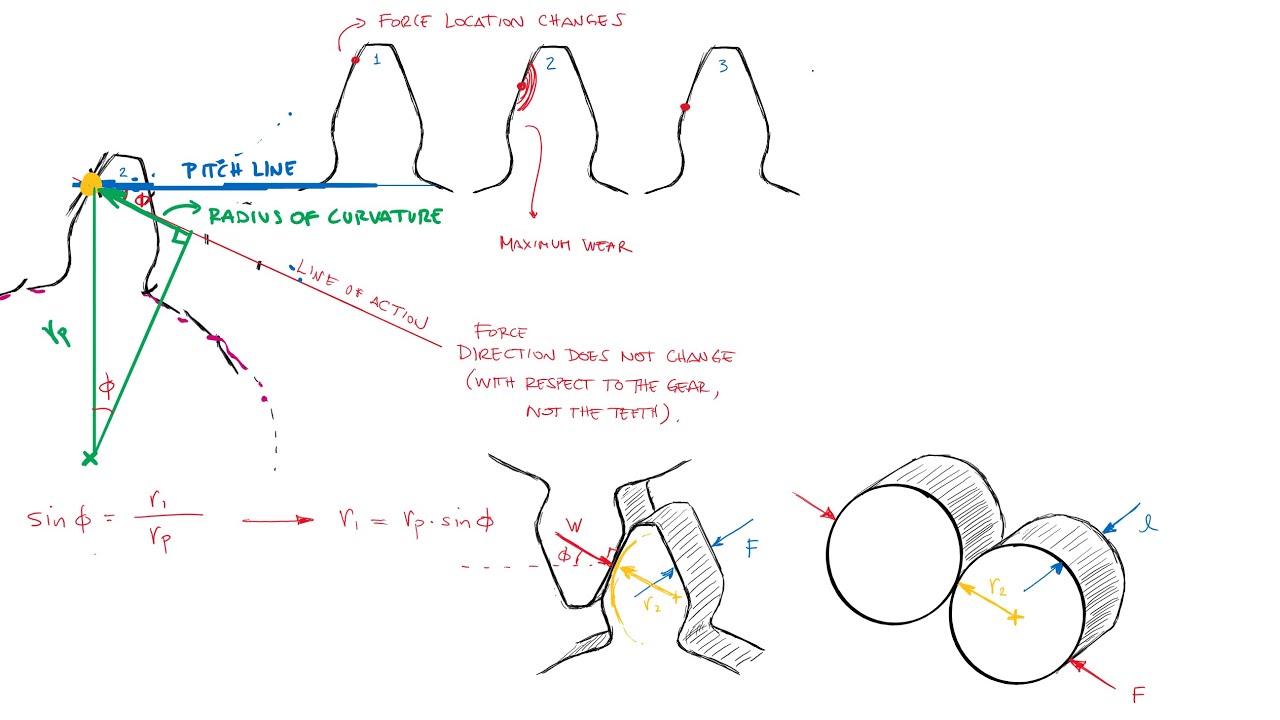
Gear PITTING - Surface Contact Stress Fatigue Failure in Just Over 10 Minutes!

Rigid Bodies: Rotation About a Fixed Axis Dynamics (learn to solve any question)

Plastik Sempurna pada Balok | Cara Menghitung Plastic Section Modulus | Struktur Baja | Lightboard
5.0 / 5 (0 votes)
