Prof C lectures on Stability: S plane ,poles and zeros
Summary
TLDRThis lesson on control engineering focuses on system stability, explaining two methods for evaluating stability: graphical and analytical. The graphical method involves plotting poles and zeros on the complex plane, while the analytical method uses mathematical equations to determine if the poles are located in the left or right half-plane. A system is stable if all poles have negative real parts. Key concepts such as transfer functions, poles, zeros, and complex numbers (sigma and omega) are explored to help identify whether a system is stable or unstable. Practical examples clarify the application of these principles.
Takeaways
- 😀 The lesson focuses on stability in control engineering, specifically determining whether a system is stable or unstable.
- 😀 Two methods for assessing stability are discussed: graphical method and analytical method.
- 😀 The graphical method involves using symbols, graphs, and descriptions to determine stability.
- 😀 The analytical method relies on mathematics and equations to evaluate system stability.
- 😀 Transfer functions are central to this analysis, with the denominator being the focus when evaluating stability.
- 😀 Stability is assessed using a plane called the Flame or PL Cartesian plane, which consists of horizontal (real) and vertical (imaginary) axes.
- 😀 The stability region is on the left half of the plane, with stable systems having poles (roots) in this region.
- 😀 A system is unstable if the poles lie in the right half of the plane, indicating positive real values.
- 😀 The script explains how to identify poles and zeros in the system using graphical symbols: circles for zeros and 'x' for poles.
- 😀 The lesson includes sample transfer functions and demonstrates how to determine the stability of systems with complex roots.
- 😀 A key takeaway is the real part of a root: if it is negative, the system is stable, and if positive, it is unstable.
Q & A
What is the main focus of the lesson on stability in control engineering?
-The main focus is on determining whether a system is stable or unstable. The lesson explores methods to analyze system stability using both graphical and analytical techniques.
What are the two methods discussed to determine if a system is stable or unstable?
-The two methods are graphical and analytical methods. The graphical method uses symbols and graphs, while the analytical method uses mathematics and equations.
What is the significance of the transfer function in analyzing stability?
-The transfer function is crucial because it allows you to evaluate the system's poles and zeros, which are key to determining stability. The focus is particularly on the denominator of the transfer function.
What is the PL Cartesian plane, and how is it used in the analysis?
-The PL Cartesian plane, also referred to as the stability plane, is a graph where the vertical axis represents imaginary values (Jω), and the horizontal axis represents real values (σ). This plane helps visualize whether a system's poles and zeros are stable.
What do the symbols 'poles' and 'zeros' represent in the context of the transfer function?
-Poles represent the roots of the denominator of the transfer function, and zeros represent the roots of the numerator. Poles indicate system stability, while zeros affect system behavior but don't directly determine stability.
How is stability determined in the graphical method?
-In the graphical method, stability is determined by checking whether the system's poles lie to the left or right of the vertical axis (representing the real axis). If poles are on the left, the system is stable; if on the right, it is unstable.
What does it mean if a system has poles with positive real parts?
-If a system has poles with positive real parts, it indicates instability. This is because positive real parts correspond to roots in the right half of the complex plane, leading to an unstable system.
How do you interpret the roots of a system's transfer function when the real part is negative?
-If the real part of the roots is negative, the system is stable because the poles lie on the left half of the complex plane, which corresponds to stable behavior in control systems.
What role do imaginary components play in the stability analysis?
-Imaginary components do not directly determine stability but can affect the oscillatory behavior of the system. The stability is primarily determined by the real part of the roots, with imaginary components indicating oscillation if present.
What does the quadratic equation have to do with stability analysis?
-The quadratic equation is used when the system’s transfer function is not easily factorable, especially when the roots cannot be found through simple factoring. The quadratic formula helps find the roots, which are essential for determining stability.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

09 PSK Routh Locus 1

#215 Problem on Nyquist plot in control systems || EC Academy
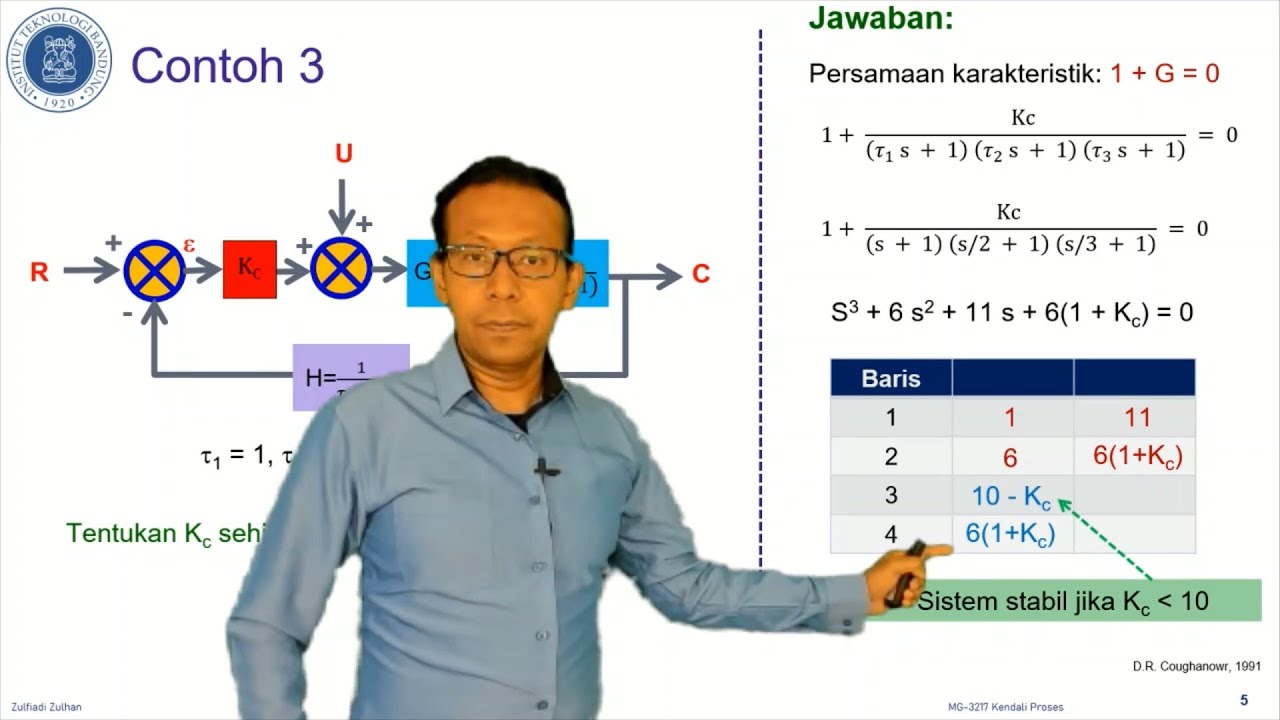
06. MG3217 Kendali Proses S04: Routh Test dan Root Locus

A PID Tuning Guide | Understanding PID Control, Part 4

Karakterisasi katalis padat

07. MG3217 Kendali Proses S02: PID Tuning, Ziegler-Nichols, Cohen-Coon (Latihan Soal))
5.0 / 5 (0 votes)
