Related Rates - Inflated Balloon & Melting Snowball Problem - Surface Area & Volume
Summary
TLDRThis video explains how to solve related rate problems involving circles and spheres, focusing on real-world scenarios like an inflating balloon and a melting snowball. It covers the principles of calculating the rates of change for circumference, area, volume, and surface area using derivatives. Key examples include finding the rate at which the circumference of a circle changes as its radius increases, how fast the area changes when the radius is altered, and determining how quickly the radius or diameter changes in spherical objects. The video emphasizes using related rate equations to solve these practical problems.
Takeaways
- 😀 The radius of a circle is increasing at a rate of 5 cm/min, and we are asked to find how fast the circumference is changing when the radius is 10 cm.
- 😀 The formula for the circumference of a circle is C = 2πr. Differentiating this with respect to time allows us to calculate the rate of change of the circumference.
- 😀 The rate of change of the circumference (dC/dt) when the radius is 10 cm is 10π cm/min.
- 😀 The rate of change of the area of a circle (dA/dt) is calculated using the formula A = πr². Differentiating with respect to time gives us the rate at which the area is changing.
- 😀 When the radius is 8 cm, the rate at which the area of the circle is changing (dA/dt) is 80π cm²/min.
- 😀 In problems involving spheres, the volume formula V = 4/3πr³ is used to calculate the rate of change of the radius when air is pumped into the balloon.
- 😀 The rate at which air is being pumped into a spherical balloon is given as 450 cm³/min. To find the rate of change of the radius (dr/dt), we differentiate the volume formula with respect to time.
- 😀 When the radius of the balloon is 10 cm, the rate at which the radius is changing (dr/dt) is 9/(8π) cm/min.
- 😀 The surface area of a melting snowball decreases at a rate of 2 cm²/min. To find how fast the diameter is changing, we relate the surface area formula (A = 4πr²) to the diameter.
- 😀 When the radius of the snowball is 5 cm, the rate at which the diameter is changing (dD/dt) is -1/(10π) cm/min, indicating the diameter is shrinking.
Q & A
What is the rate at which the circumference of the circle is changing when the radius is 10 centimeters?
-The rate at which the circumference is changing is 10π centimeters per minute. This is found by differentiating the formula for circumference, C = 2πr, with respect to time and using the given rate of change of the radius (dr/dt = 5 cm/min).
What is the relationship between the rate of change of the area and the radius of a circle?
-The rate of change of the area, dA/dt, is related to the radius through the formula A = πr². By differentiating this formula with respect to time, you get dA/dt = 2πr(dr/dt), where r is the radius and dr/dt is the rate of change of the radius.
How do you calculate the rate of change of the area when the radius is 8 centimeters?
-The rate of change of the area (dA/dt) when the radius is 8 centimeters is calculated by differentiating the area formula A = πr². Substituting r = 8 and dr/dt = 5 cm/min gives dA/dt = 80π square centimeters per minute.
What formula connects the volume of a sphere to its radius?
-The volume of a sphere is connected to its radius by the formula V = (4/3)πr³. Differentiating this with respect to time allows you to find the rate of change of the volume (dV/dt) in terms of the rate of change of the radius (dr/dt).
How do you calculate the rate at which the radius of a spherical balloon is changing?
-To find the rate at which the radius is changing (dr/dt) when the volume of the balloon is changing, differentiate the volume formula V = (4/3)πr³. After substituting the given rate of change of volume (dV/dt = 450 cm³/min) and the radius (r = 10 cm), you can solve for dr/dt.
What units are used when calculating the rate of change of the area of a circle?
-The units for the rate of change of area are square centimeters per minute (cm²/min). This comes from differentiating the area formula A = πr², which results in an area change over time, where r is measured in centimeters and time is in minutes.
What is the significance of a negative rate of change in related rates problems?
-A negative rate of change indicates a decrease in the quantity being measured. For example, in the melting snowball problem, a negative rate for the surface area (dA/dt = -2 cm²/min) means the snowball's surface area is shrinking over time.
How is the diameter of a snowball related to its radius in the melting snowball problem?
-The diameter of a snowball is always twice the radius, i.e., D = 2r. This relationship is used to derive an equation for the surface area of the sphere in terms of the diameter, which can then be differentiated to find the rate of change of the diameter (dD/dt).
Why is the formula for the surface area of a sphere, 4πr², used in the melting snowball problem?
-The formula for the surface area of a sphere, 4πr², is used because it directly relates to the snowball's changing size. By differentiating this equation with respect to time, you can find the rate at which the surface area is changing (dA/dt), which is given in the problem.
How do you calculate the rate of change of the diameter of a melting snowball when the radius is 5 cm?
-To calculate the rate of change of the diameter (dD/dt) when the radius is 5 cm, first relate the surface area formula to the diameter using D = 2r. Differentiate the surface area formula with respect to time and solve for dD/dt. With dA/dt = -2 cm²/min and D = 10 cm, the result is dD/dt = -1/(10π) cm/min.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
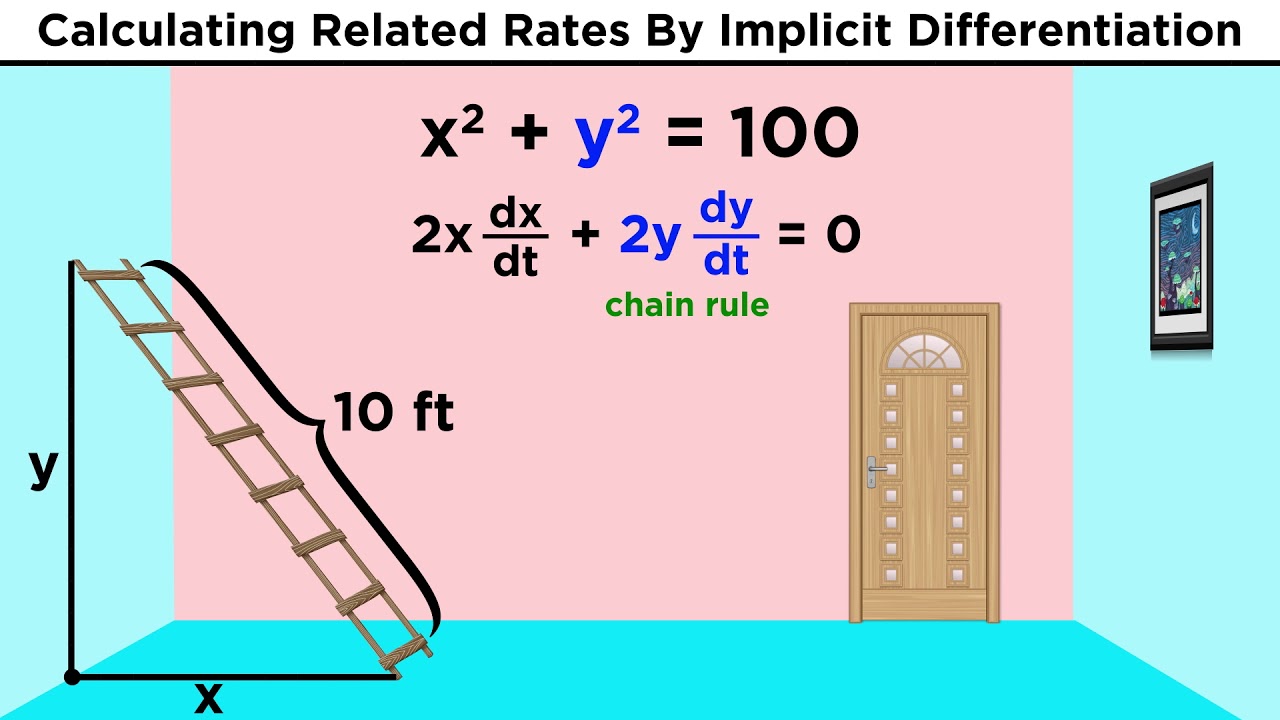
Related Rates in Calculus

Review on Circles

Application of Derivatives: Related Rates (Inflating Balloon, Draining Water on a Tank) - Calculus
Circle Theorems questions - Corbettmaths

Solving For Commission and Commission Rate | Grade 7 | Matatag Curriculum | Explain in Detailed |

Matematika Kelas 9: Bangun Ruang Sisi Lengkung (Tabung, Kerucut, Bola)
5.0 / 5 (0 votes)
